22.04.2022 Unternehmen und Rationalkalkül#

Gegenseite zur Haushalte und Nachfrage: Unternehmen und Angebot

Annahmen:

  • Kosten C

  • Inputs/Faktoren \(r_1,r_2\) mit Preisen \(q_1,q_2\), oft:

    • \(r_1\) = Arbeit mit Lohn \(q_1\)

    • \(r_2\) = Kapital mit Zins \(q_2\)

  • Maximierung von Gewinn G

Isoquantenfunktion#

aus Inputs \(r_1,r_2\) wird Gut x hergestellt in Produktionsfunktion \(x(r_1,r_2)\)

  • jedes weitere eingebrachte Input steigert, aber mit abnehmenden Grenzertrag

Produktionskurve für ein Gut: 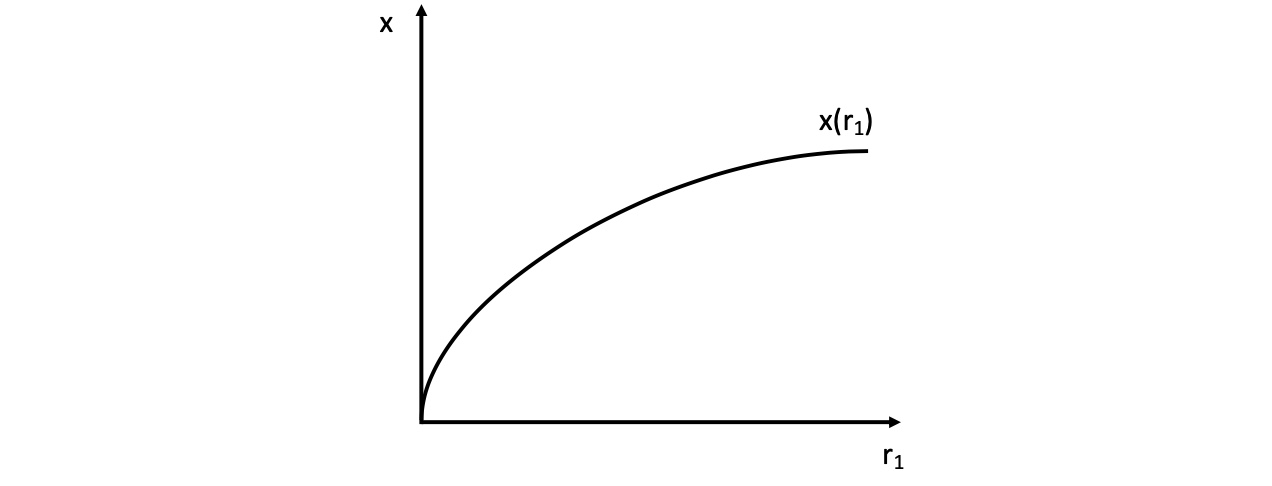2022-04-22_20.29.15

  1. Ableitung = Grenzproduktivität > 0

  2. Ableitung = Steigerung der Grenzprod. < 0

für Güterkombination: Isoquantenkurve (iso = gleich, quant = Menge -> gleiche Menge)

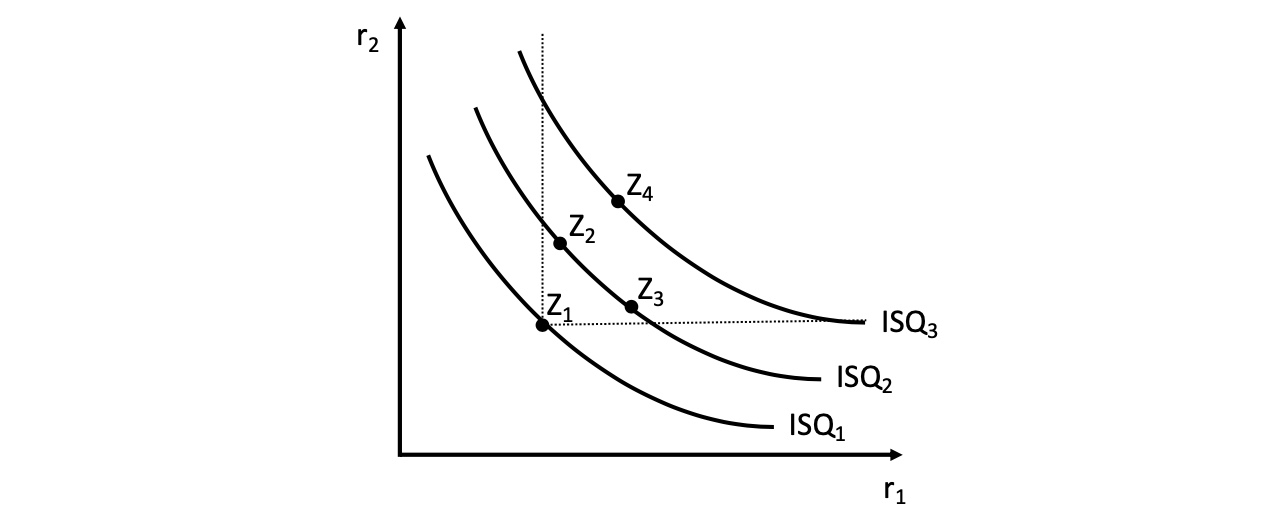
2022-04-22_20.37.08

Bilden des totalen Differentials und umstellen: $$ \text{Grenzprod. * Veraenderung erster Faktor + …} \

\to dx = \frac{\partial x}{\partial r_1} * \Delta r_1 + \frac{\partial x}{\partial r_2} * \Delta r_2 \

\frac{\Delta r_2}{\Delta r_1} \bigg|_T = -\frac{\frac{\partial x}{\partial r_1}}{\frac{\partial x}{\partial r_2}} = MRTS \text{ (Marginal Rate of Technical Subst.)} $$

hier sind das die Opportunitätskosten von \(r_1\) (eine Einheit mehr von \(r_1\), wieiviel Verzicht auf \(r_2\))

MRTS: Grenzrate der technischen Substitution, beschreibt technisches Substitutionskönnen des Unternehmens

Isokostengerade#

Kostenfunktion eines Unternehmens: \(C = q_1 * r_1 + q_2 * r_2\)

  • unter Annahme eines perfekten Marktes

Darstellung mit Isokostengerade: 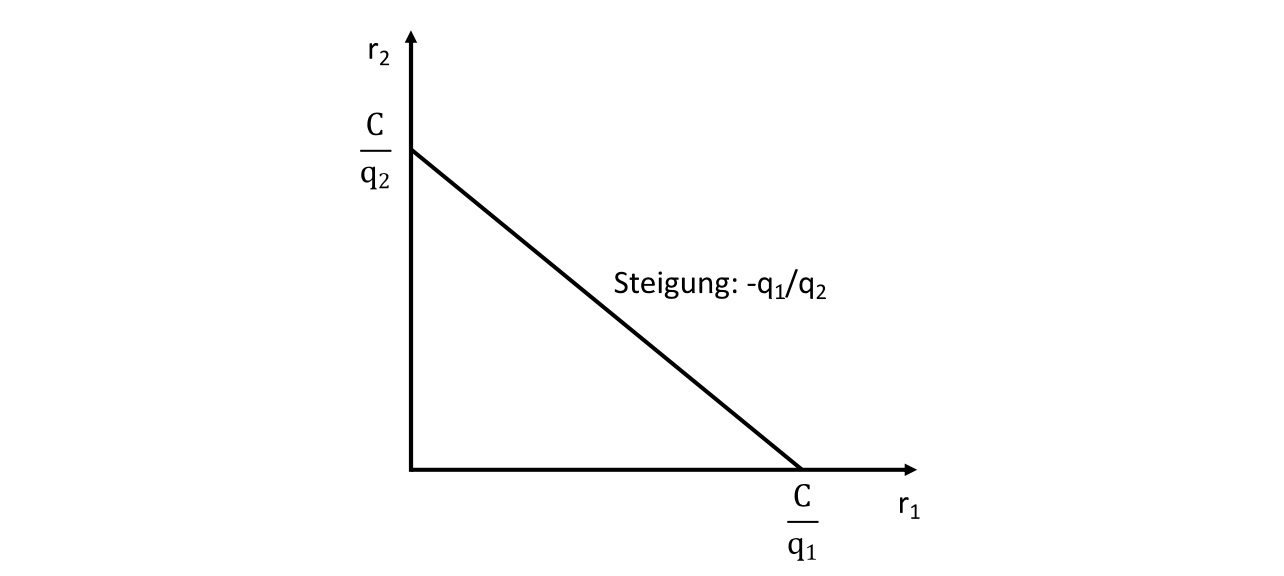2022-04-22_21.01.02

MRMS: (Marginal Rate of Market Substitution) das Preisverhältnis zweier Güter

Produktionsgleichgewicht#

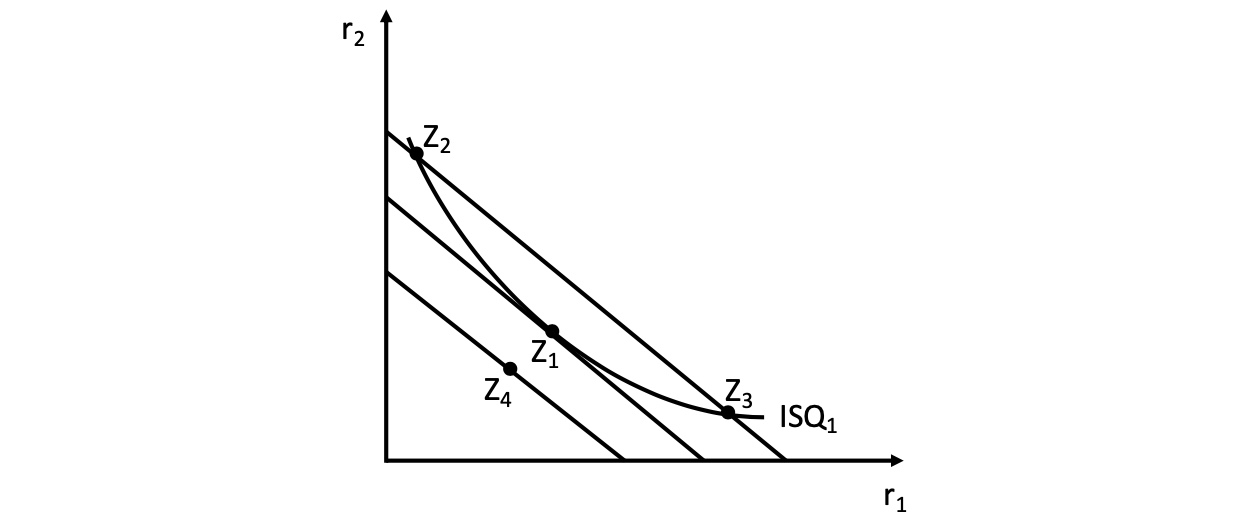
2022-04-22_21.02.58

in optimalen Punkt \(Z_1\) ist \(|MRTS| = |MRMS| \)

Betrachtung mit Lagrange-Funktion $\( L = x(r_1,r_2) + \lambda * (C- r_1*q_1 - r_2 *q_2) \)$

  • der hintere Summand ist bei rationalen Unternehmen 0

    • alles Geld wird verwendet für Faktoren

  • \(\lambda\) = Grenznutzen des Geldes

    • wieviel mehr x wenn C um 1 Euro erhöht wird

    • = erste Ableitung der Zielfunktion \(\frac{\partial x}{\partial C}\)

Ableitung der Lagrange Funktion $\( \to \frac{\partial L}{\partial r_1} = \frac{\partial x}{\partial r_1} - \lambda*q_1 = 0 \\ \to \frac{\partial L}{\partial r_2} = \frac{\partial x}{\partial r_2} - \lambda*q_2 = 0 \\ \to \frac{\partial L}{\partial \lambda} = C- r_1*q_1 - r_2 *q_2 \)$

Exkurs marginale Zahlungsbereitschaft#

MZB: persönliche Bereitschaft zu Zahlung eines Preis

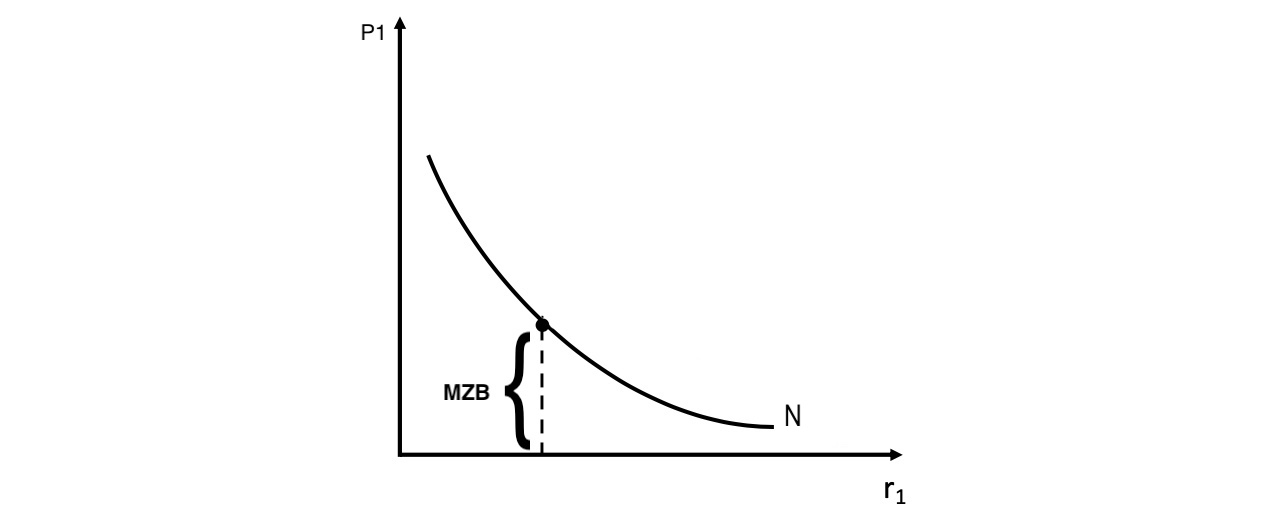22-04-22_21-42 $\( P_1 = \frac{\frac{\partial U}{\partial x_1}}{\lambda} = MZB \)$

  • \(\lambda\) ist Faktor und U verändert sich => abnehmender Grenznutzen

  • bei Menschen ohne Geld ist Grenznutzen des Geldes \(\infty\)

    • Dadurch \(\lambda = \infty\) und MZB = 0

    • nur wenn Subsistenzeinkommen für Marktteilnehmer können sie sich überhaupt etwas kaufen

    • deswegen Sozialstaat!

Expansionspfad#

beschreibt Verhältnis zwischen Inputs-Outputs, die bei Unternehmen nach oben offen sind (langfristig)

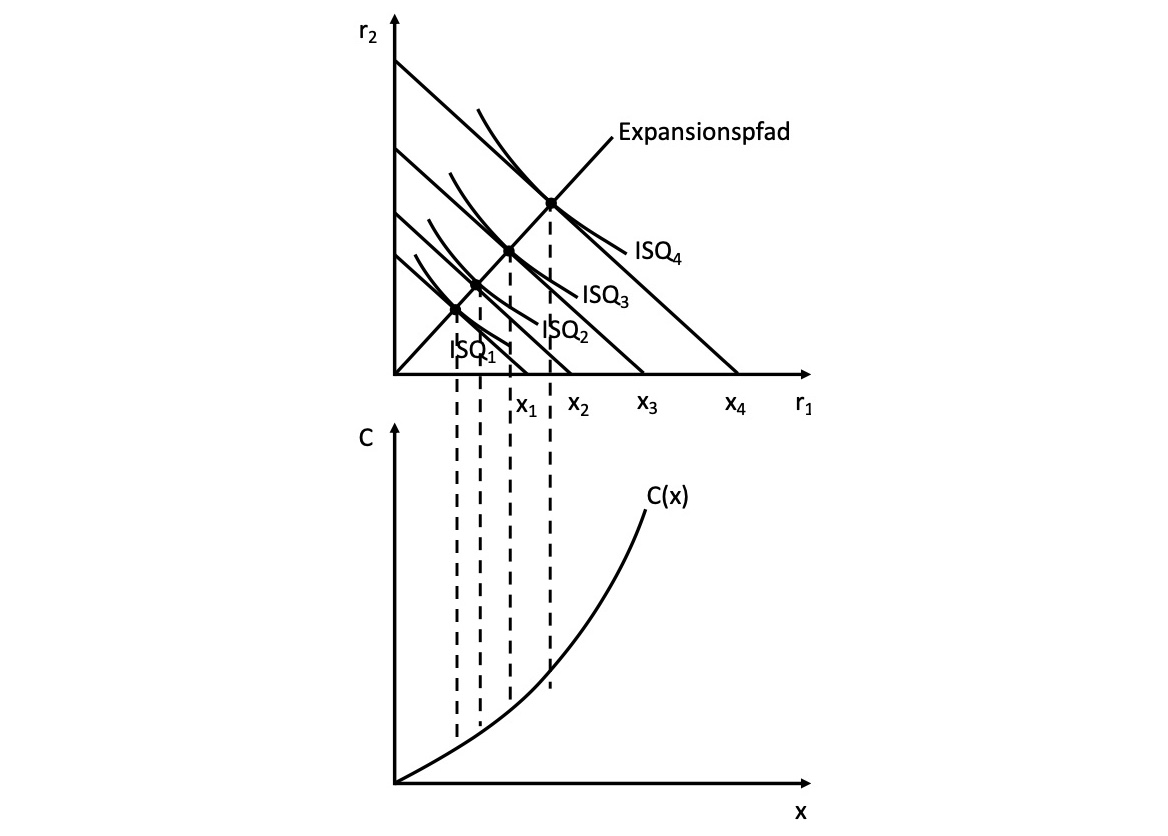
2022-04-22_21.54.15

Gewinnmaximierung#

Gewinn = Erlös - Kosten: \(G(x) = E(x) - C(x)\)

  • Maximum bei \(\frac{\partial G}{\partial x} = \frac{\partial E}{\partial x} - \frac{\partial C}{\partial x} = 0\)

  • Grenzgewinn ist null und Grenzerlöse = Grenzkosten

nach Einsetzen der Erlösfunktion \(p = \frac{\partial C}{\partial x}\)

  • Preis für Gut = Grenzkosten

Übung#

Isoquante#

Beispiel-Produktionsfunktion \(x (L,K) = L^{0,5} K^{0,5}\)

Punkte:

  1. (2,8)

  2. (3,12)

  3. (8,2)

  4. (12,3)

Nutzen der Punkte (Einsetzen in x)

  1. x = 4

  2. x= 6

  3. x = 4

  4. x = 6

Gleichung der Isoquanten hier: \(K = \frac{x^2}{L}\)

  • Erste Outputfunktion x= 6 \(\to \frac{36}{L}\)

  • x = 4 \(\to \frac{16}{L}\)

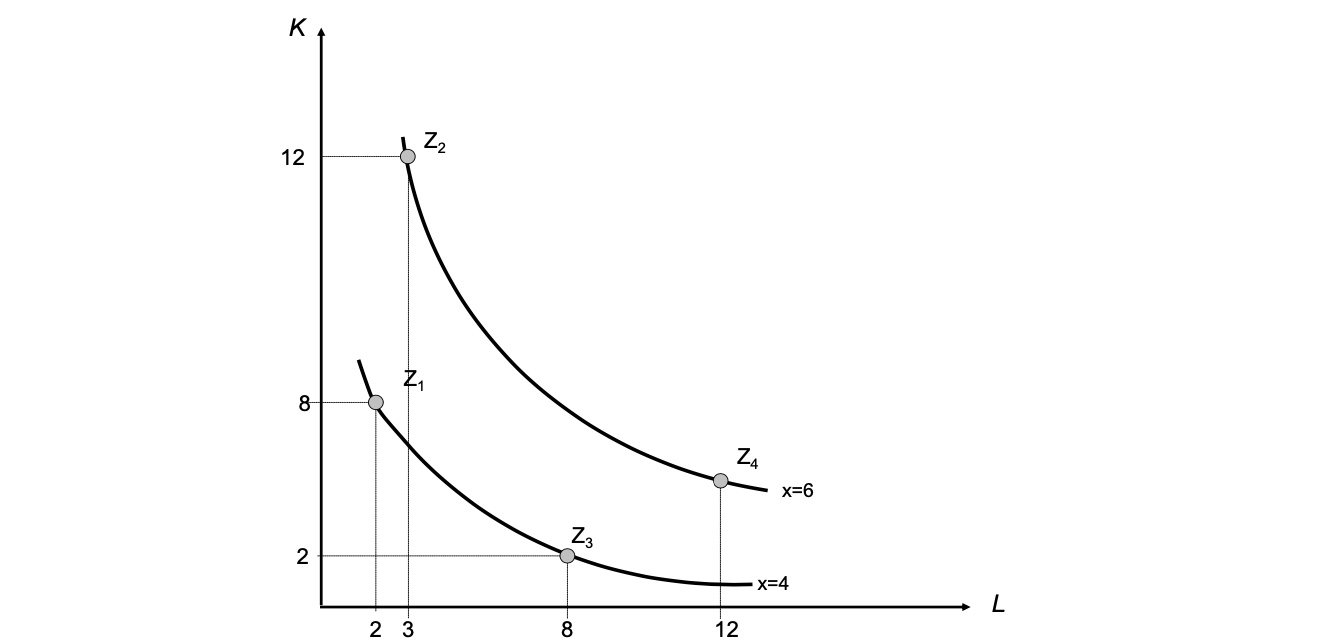
2022-05-09_14.50.27

Grenzproduktivitäten:

  • der Arbeit: \(MP_L = \frac{\partial x}{\partial L} = \frac{1}{2} \sqrt{\frac{K}{L}}\)

  • des Kapitals: \(MP_K = \frac{\partial x}{\partial K} = \frac{1}{2} \sqrt{\frac{L}{K}}\)

Steigung der Isoquante $\( Funktion: K = \frac{x^2}{L} \\ Ableitung: \frac{\partial K}{\partial L} = - \frac{x^2}{L^2} \)$

die Ableitung ist die Steigung der Isoquante = MRTS

Effekt von gestiegener Arbeitsproduktivität:

Marginal Rate of Market Substituions: (andere Formel) \(MRTS = \frac{MP_L}{MP_K} = -\frac{\frac{\partial x}{\partial L}}{\frac{\partial x}{\partial K}} \) $\( Effekt: MRTS \uparrow= \frac{MP_L \uparrow}{MP_K} \)$ = größere Steigung = steilerer Anstieg der Isoquante

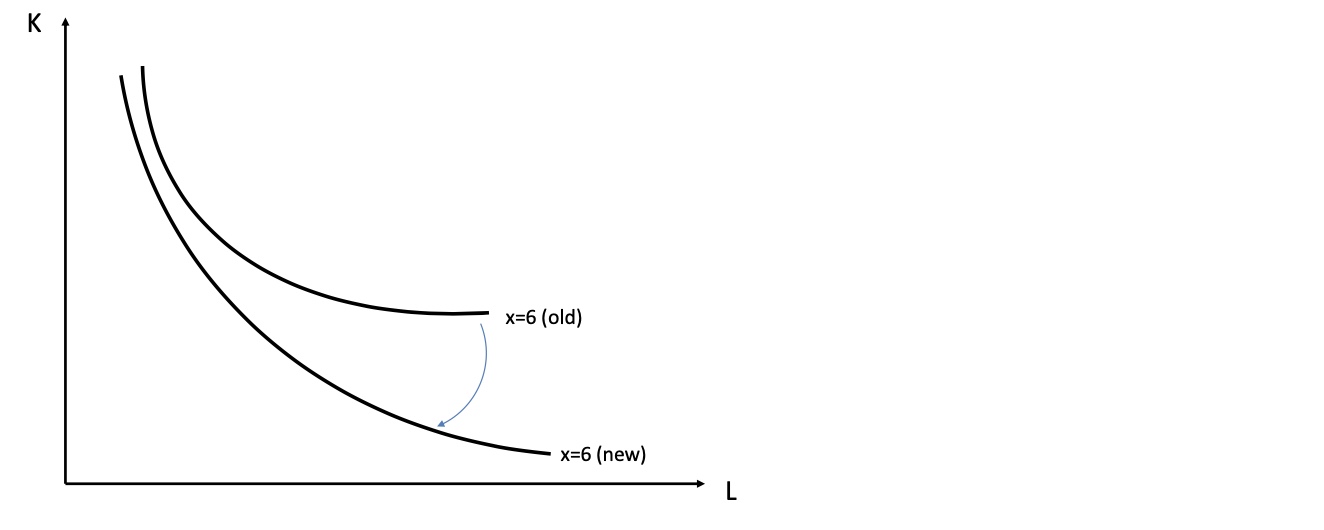
2022-05-09_15.00.59

analog Steigung der Produktivität des Kapitals: \(Effekt: MRTS \downarrow= \frac{MP_L}{MP_K \uparrow}\)

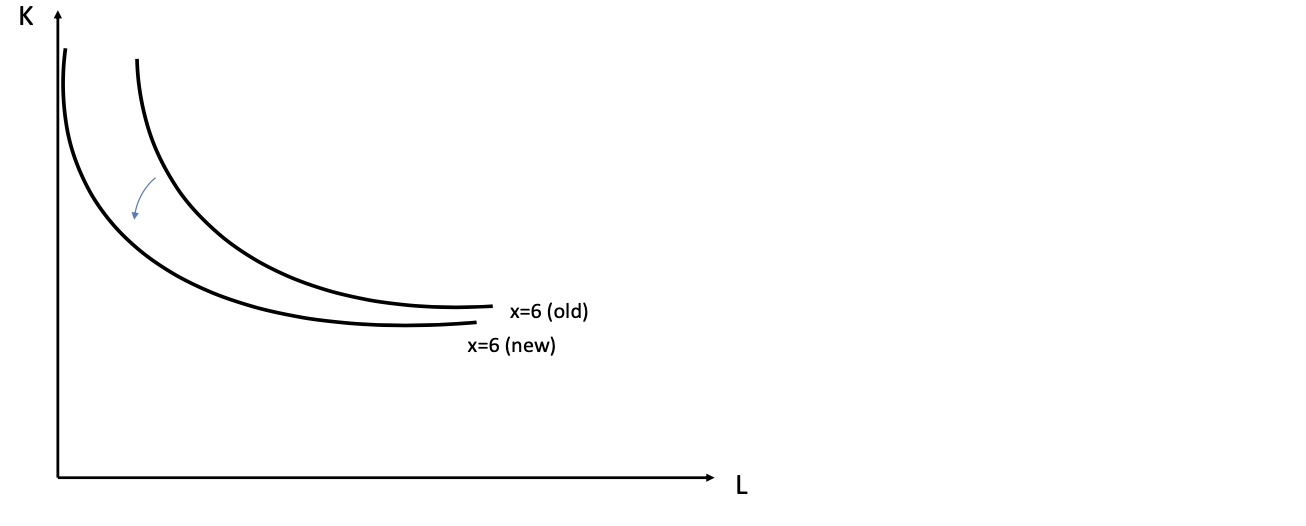
2022-05-09_15.03.52

Isokosten#

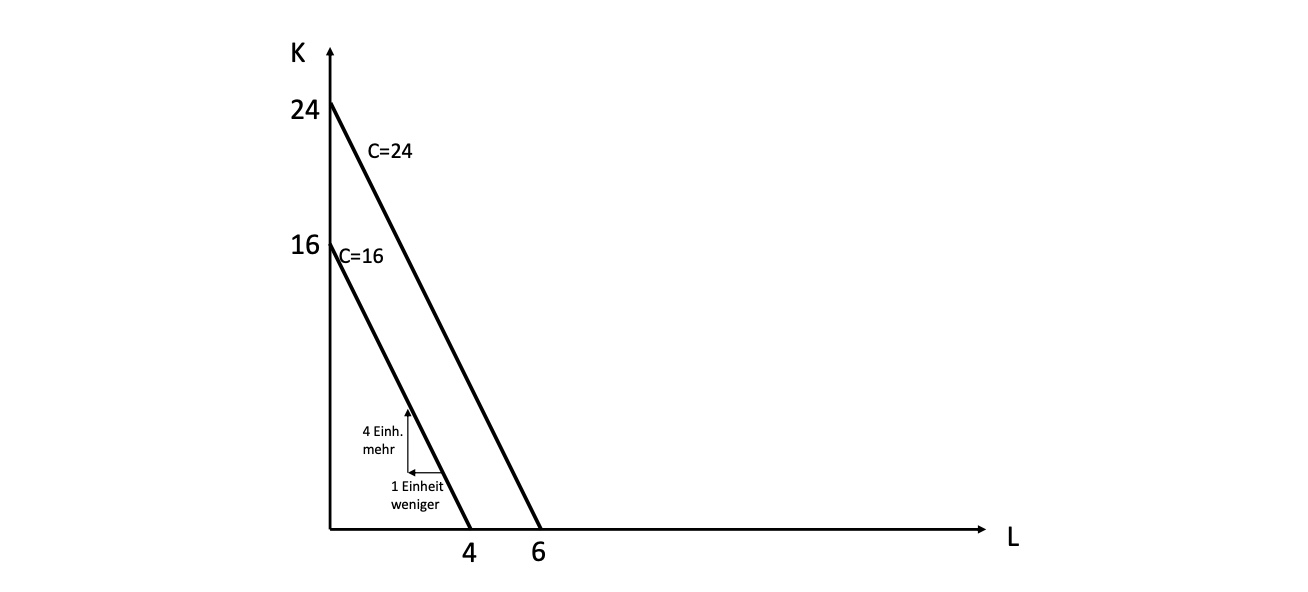
  • Kostenfunktion generell: \(C = wL+qK\)

    • bei w = 4, q=1 und C = 16

    • \(16 = 4L + K\)

  • Funktionsumstellung: \(K = -\frac{w}{q}L+\frac{C}{q}\)

    • \(K = -4L + 16\)

Schnittpunkte:

  • Ordinate: \(\frac{C}{q} = 16\)

  • Abszisse: \(\frac{C}{w} = 4\)

Steigung der Kostenfunktion = \(\frac{\partial K}{\partial L} = \big|-\frac{w}{q} \big| = \frac{w}{q}\)

  • Hier: -4 (Kosten der Arbeit in Einheiten von Kapital)

  • Ist MRMS (Marginal Rate of Market Subst.)

Graphisch: (mit noch anderen Kostenniveau)

2022-05-09_15.09.20

Kostenminimum mit Lagrange-Funktion#

Kostenminimum analytisch!

1: Aufstellen des Optimierungsproblems#

\[\begin{split} min_{L,K} \ C = min(wL+qK) \\ s.t \\ L^{0,5} K^{0,5} = x \end{split}\]

2: Aufstellen der Lagrange Funktion#

\[ LF = (wL+qK)+\lambda(x-L^{0,5}K^{0,5}) \]

3: Ableiten der Lagrange Funktion (nach \(L,K, \lambda\) )#

\[\begin{split} \frac{\partial LF}{\partial L} &= w- \lambda \frac{K^{0,5}}{2L^{0,5}} = 0 \\ \frac{\partial LF}{\partial K} &= q- \lambda \frac{L^{0,5}}{2K^{0,5}} = 0 \\ \frac{\partial LF}{\partial \lambda} &= x- L^{0,5}K^{0,5} = 0 \end{split}\]

4: Lösen des LGS#

  • Auflösen der ersten und zweiten nach Lambda

\[ \begin{align}\begin{aligned}\begin{split} \frac{\partial LF}{\partial L} \implies \lambda = 2w \frac{L^{0,5}}{K^{0,5}} \\\end{split}\\\frac{\partial LF}{\partial K} \implies \lambda = 2q \frac{K^{0,5}}{L^{0,5}} \end{aligned}\end{align} \]

  • Gleichsetzen und auflösen nach Menge Arbeit

\[\begin{split} 2w \frac{L^{0,5}}{K^{0,5}} = 2q \frac{K^{0,5}}{L^{0,5}} \\ L = \frac{q}{w} K \end{split}\]

  • Einsetzen in dritte Gleichung

\[\begin{split} x - \bigg(\frac{q}{w}K \bigg)^{0,5}K^{0,5} = 0 \\ K = x \bigg( \frac{w}{q}\bigg)^{0,5} \end{split}\]

= kostenminimaler Einsatz von Kapital

  • Einsetzen davon in Restriktion

\[ L = x \bigg( \frac{q}{w} \bigg)^{0,5} \]

= kostenminimaler Einsatz von Arbeit

  • Bestimmung des Optimums für Output x=4

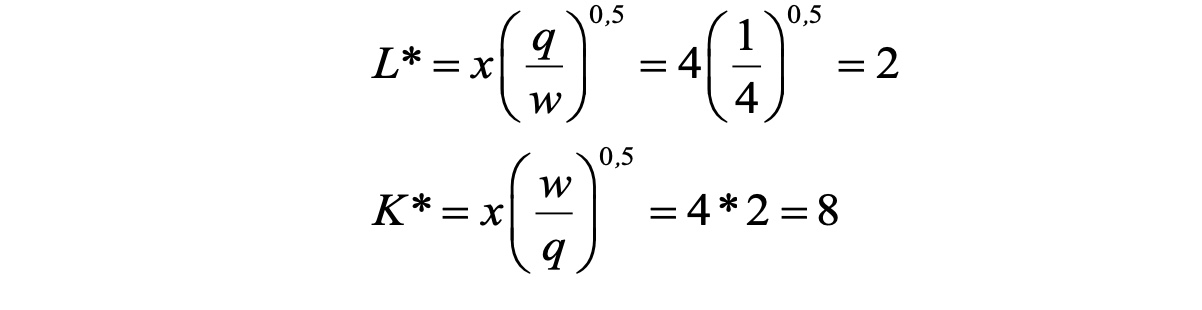
2022-05-09_15.29.42

Kostenmimimum graphisch#

im Mimimum: \(\frac{MP_L}{MP_K} = MRTS = MRMS = \frac{w}{q}\)