25.10.2022 Solow II und Humankapital

Erweiterung des Solow Modells

Bevölkerungswachstum

Annahme: konstantes Wachstum der Bevölkerung mit Rate n: \(L(t) = L(0) \cdot e^{nt}\)

Dann Veränderung des Pro-Kopf-Kapitalstocks: $\( \frac{\dot{k}}{k}=s\frac{y}{k}-\delta - \bf{n} \\ \to \dot{k} = sy-(n+\delta)k \)$ => Bevölkerungswachstum heißt weniger Pro-Kopf-Kapital = weniger Wachstum

Steady State: (jeweils im Nenner nur das n zu \(\delta\) addiert) $\( k^* = \Big(\frac{s}{n+\delta}\Big)^{\frac{1}{1-a}} \\ y^* = (k^*)^a = \Big(\frac{s}{n+\delta}\Big)^{\frac{a}{1-a}} \)$ => Bevölkerungswachstum heißt niedrigerer Steady State

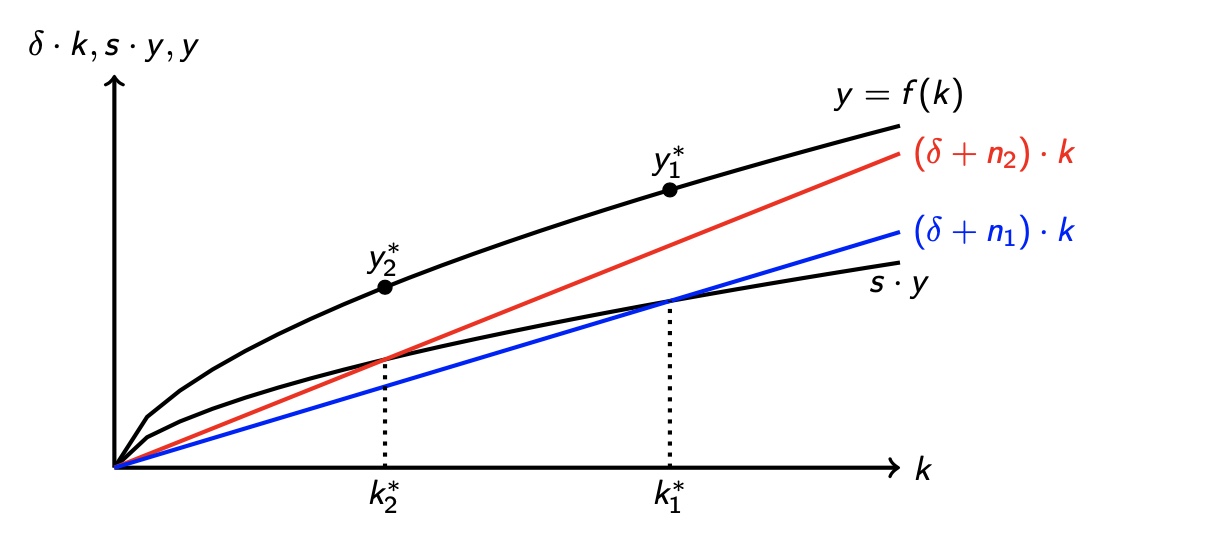
Technologischer Fortschritt

Fortschritt = Skalierungsfaktor in Cobb-Douglas-Produktionsfunktion = Technologieniveau $\( Y = F(A,K,L) = F(K,A\cdot L) = K^a (AL)^{1-a} \)$

• Fortschritt hilft Arbeit = labor-augmenting techn. progress

• bei Cobb-Douglas aber irrelevant: \(Y = A \cdot F(K,L)\)

• Wachstum von A mit konstanter Rate g: \(A_t = A_0 \cdot e^{gt}\)

Einkommen und Pro-Kopf-Einkommen: $\( Y = K^a (AL)^{1-a} \\ \implies y = k^a A^{1-a} \)\( Insgesamt: **Wachstumsrate A = Wachstumsrate y** \)\( \frac{\dot{k}}{k} = \frac{\dot{y}}{y} = \frac{\dot{A}}{A} = g \)$ = balanced growth path

Steady State = Kapitalstock pro effektivem Arbeiter $\( \tilde{k}^* = \frac{k}{A} = \Big(\frac{s}{n+\delta+g}\Big)^{\frac{1}{1-a}} \\ \tilde{y^*} = (\tilde{k}^*)^a = \Big(\frac{s}{n+\delta+g}\Big)^{\frac{a}{1-a}} \)$

echtes Pro Kopf = nicht effektiver arbeiter, also alles mit A multiplizieren

A bekommen wir aus Produktionsfunktion $\( Y = K^a (AL)^{1-a} \\\to A= \Big(\frac{Y}{K^a L^{1-a}}\Big)^{\frac{1}{1-a}} \\ y^* = A \cdot (k^*)^a = A \cdot\Big(\frac{s}{n+\delta+g}\Big)^{\frac{a}{1-a}} \)$

Insgesamt:

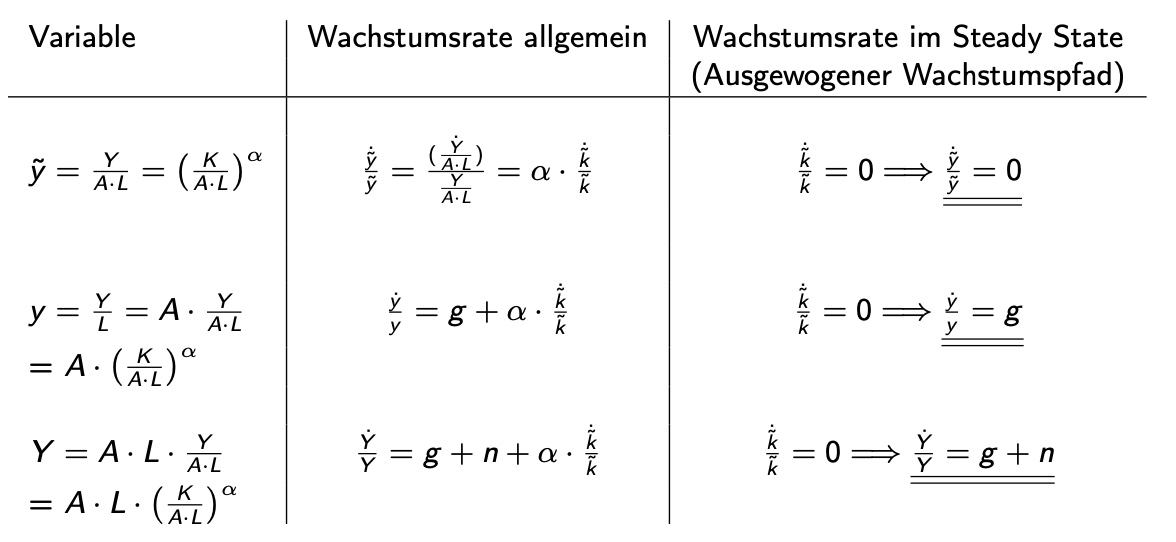
Humankapital

im Solow Modell wirt zwischen den Arbeitskräften nicht unterschieden (Bildungslevel)

• beispielsweise anhand der Länge der Schulbildung

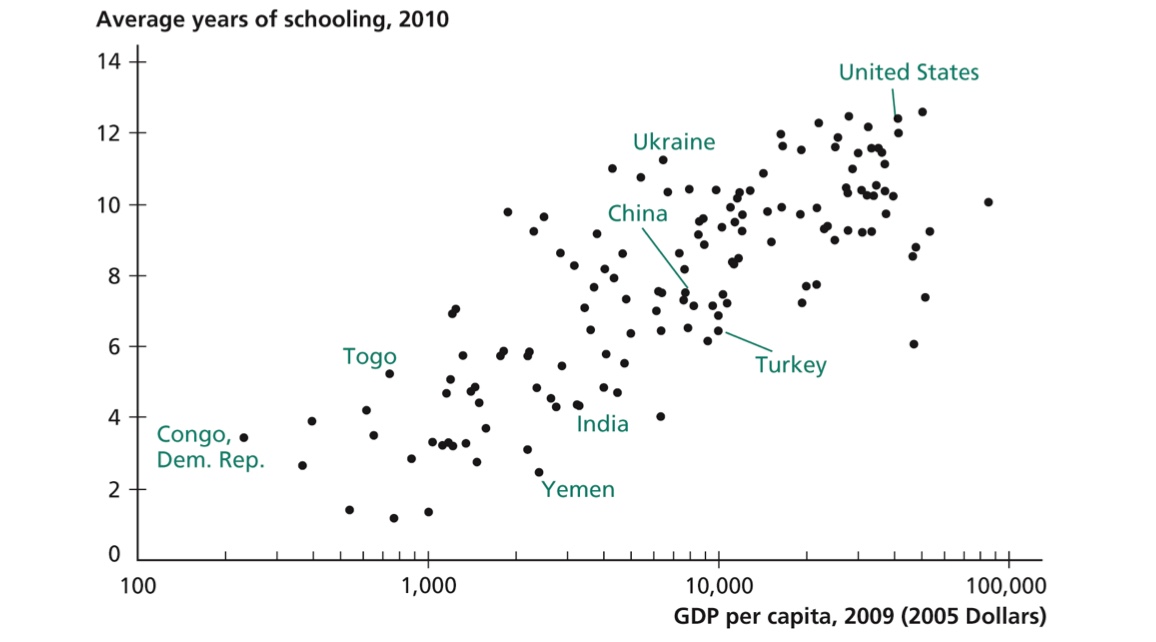
Humankapital nach Mincer

\[ Y = K^a (AH)^{1-a} \text{ mit } H = e^{\psi \cdot u} L \]

also gehen ungelernte Arbeiter:innen L für u Jahre zu Schule und realisieren \(\psi\) Returns on Education pro Bildungsjahr

• \(\psi\) wird meist mit 0.1 angenommen = 10% pro Jahr

\[\begin{split} y = k^a (A \cdot h)^{1-a} \\ \text{ mit } h = \frac{H}{L}=e^{\psi u} \end{split}\]

Ähnlich wie vorher wird ProKopf Einkommen mit \(A \cdot h\) multiplizieren $\( y^* = Ah \cdot (k^*)^a = Ah \cdot\Big(\frac{s}{n+\delta+g}\Big)^{\frac{a}{1-a}} \\ \frac{k}{Ah} = \text{Effektive Gelernte Arbeiter:in} \)$

Humankapital nach Mankiw/Romer/Weil

schlagen andere Einbeziehung vor:

• ungelernte Arbeiter:in L

• gelernte Arbeiter:in H

Humankapital ähnlich physischem K.,

• man kann in Bildung investieren \(s_h\)

• oder in physischem Kapital \(s_k\)

nicht durcheinander beschrieben wie bei Mincer $\( Y = K^a H^b (AL)^{1-a-b} \\ \to y^*(t) = A(t) \Big[ \Big( \frac{s_k}{n+\delta+g}\Big)^a \Big( \frac{s_h}{n+\delta+g}\Big)^b \Big]^{\frac{a}{1-a-b}} \)$

Vergleich beider Ansätze

beide sind gleich, wenn alle Arbeit ungelernt

• \(\beta\) = 0 (Romer)

• \(u= 0 \to e^{u}=0\)