11.10.2022 Wachstum 1

BIP

BIP per Capita

Vorteile	Nachteile
Standardisierung	Vernachlässigung Externalitäten
Vergleichbarkeit	Verteilung nicht berücksichtigt
Einfach ermittelbar	Verkürzung auf Neuproduktion
einfach verständlich	kein Preis/Gut = kein Einfluss

Definition: Konsum + Investitionen + Staatsausgaben+ Netto Exporte

Alternativer Ansatz: GDP-B (Benefits)

• Nutzenmessung, die (digitale) Güter bringen

• über Befragung, wieviel Nutzer bezahlt werden müssten um nicht drauf zu greifen zu können

Alternative: HDI

HDI: Human Development Index, Indikator entwickelt von der UN, beihnaltet Lebenserwartung, Bildung, Einkommen

\(HDI=(I_{Life} \cdot I_{Education} \cdot I_{Income})^{1/3}\)

Top 5:

1. Norwegen

2. Schweit

3. Irland

4. Hongkong

aber immer noch vergleichswise starke Korrelation mit BIP

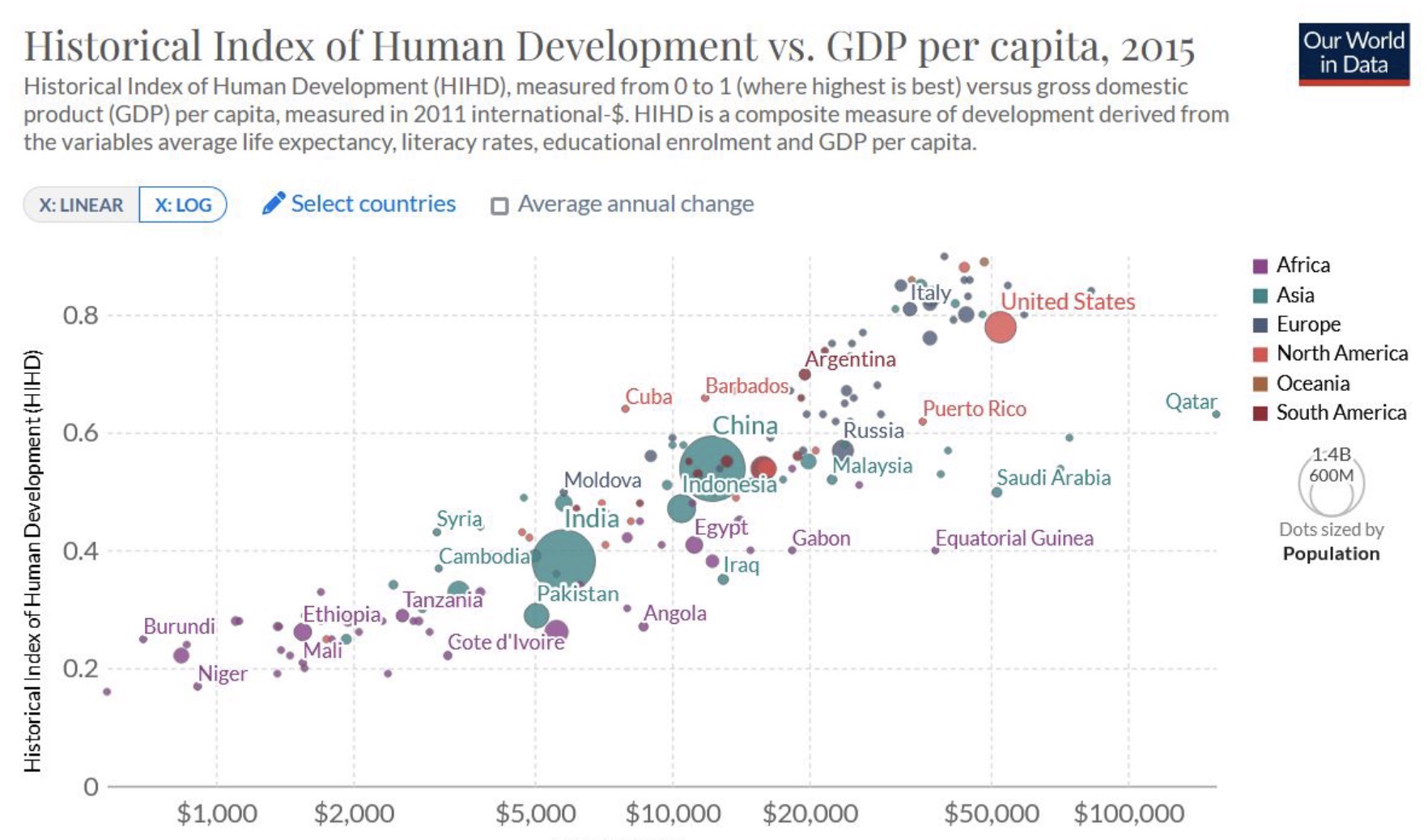
Fakten

1. BIP p.P in ärmsten Ländern ist 5% der reichsten

2. Wachstumsraten variieren erheblich

3. Wachstumsraten sind nicht konstant

Wachstum

in den letzten 50 Jahren insbesondere in Asien

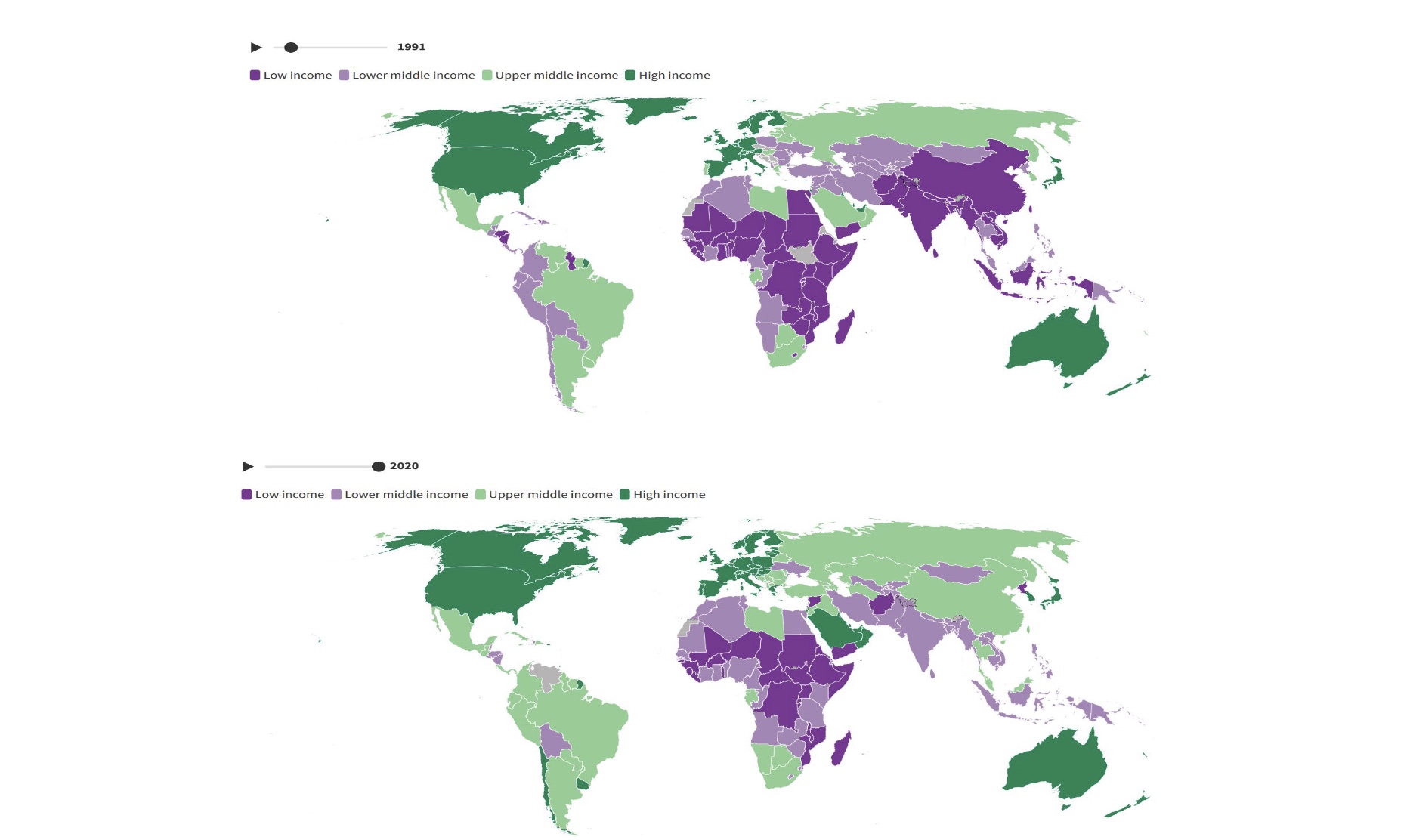
Wachstumsarten

1. Diskretes Wachstum: Anfang der Periode \(Y_0\) und Ende der Periode \(Y_1\)

   • \(Y_1 = Y_0 \cdot (1+g)\)

   • \(g = \frac{Y_1}{Y_0}-1 = \frac{Y_1-Y_0}{Y_0}\)

   • bei T Wachstumsperioden = Multiplikativ: \(Y_T = Y_0 * (1+g_1)*(1+g_2)...\)

   • Wachstumsrate: \(g = \Big(\frac{Y_T}{Y_0} \Big)^{1/T} - 1\)

2. kontinuierliches Wachstum: eher wie mit Zinseszins, immer von letztem Ausgansstandpunkt

   • zerlege Wachstumsperiode in n Zeitintervalle

   • je mehr n, desto größer Gesamtwachstum = Zinseszinseffekt durch häufige Kapitalisierung

Transformation und \(n \to \infty\) $\( Y_1 = Y_0 \cdot (1+ \frac{g}{n})^n & \bigg| \text{ Ersetze } \frac{g}{n}= \frac{1}{m} \\ \implies \underline{Y_1 = Y_0 \cdot e^g} \\ g = \ln(Y_1) - \ln(Y_0) \)$ Unterschiede verschwinden:

• Kleiner Beobachtungszeitraum

• kleine Wachstumsrate

\[ \text{Approximation }\to \ln(Y_1) - \ln(Y_0) \approx \frac{Y_1-Y_0}{Y_0} \]

Wachstumsmodelle nutzen kontinuierliches Wachstum!

bei sehr kleinen Zeitintervallen = Ableitung: \(g= \frac{\delta \ln(Y)}{\delta t}\)

Produktionsfunktion

Cobb-Douglas-Funktion: \(Y = K^a L^{1-a} \\\) $\( \begin{aligned} ln(Y) &= ln(K^a) + ln(L^{1-a}) \\ &= a * ln(K) + (1-a) * ln(L) \\ \implies \frac{\delta ln(Y)}{\delta t} &= a * \frac{\delta ln(K)}{\delta t} + (1-a) * \frac{\delta ln(L)}{\delta t} \\ \end{aligned} \)\( Term \)\frac{\delta ln(K)}{\delta t}$ ist Wachstumsraten des Kapitals

Logarithmen sind praktisch für Wachstumsraten

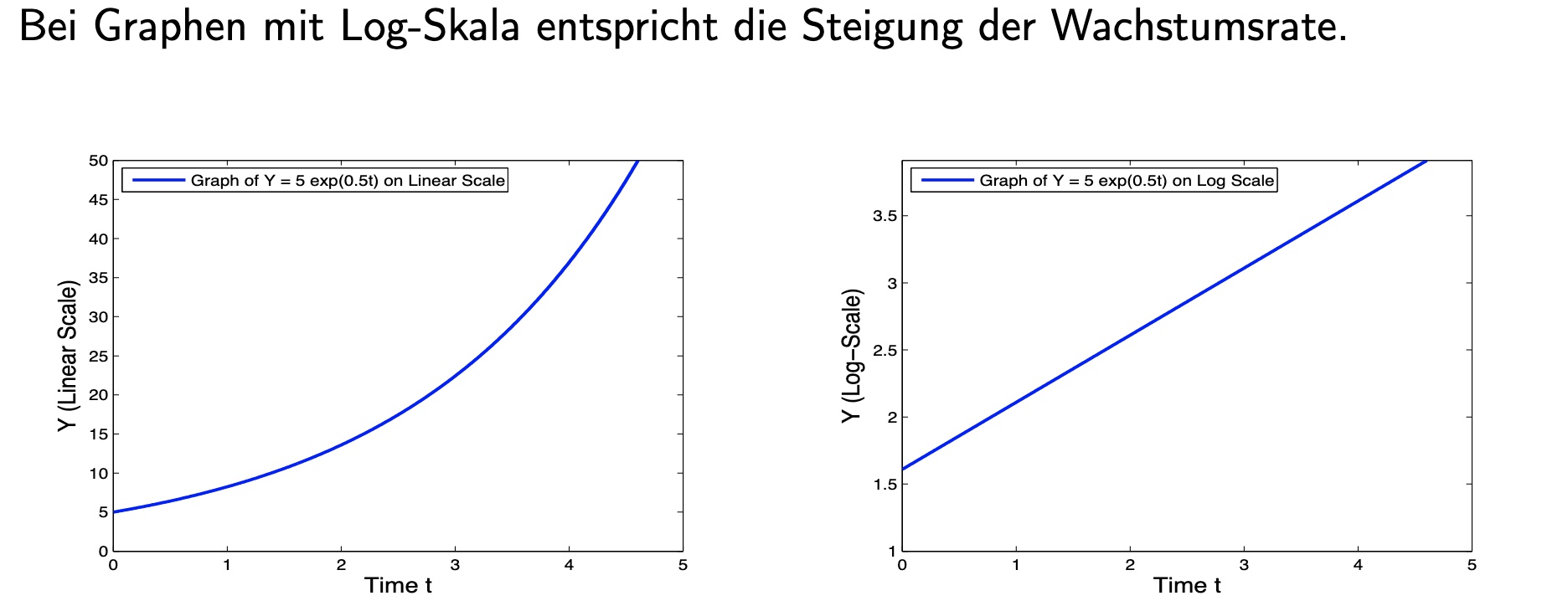
Übung 1

a)

• BIP:Summe der Produkte, die in einem Land in Zeitperiode hergestellt wurden

• Pro Kopf BIP

  • Vorteile: einfach berechenbar, verständlich

  • Nachteile: nicht bepreiste Güter = kein Eingang, Verteilung

• Nutzen der Digitalwirtschaft = nicht immer bereits = untererfassung

  • Konsumentennutzen über GDP-B (Benefits)

b)

• \(I_{life} = 8/13\)

• \(I_{Income} = 0.35148\)

• \(I_{Education} = 0.4222\)

• \(HDI = 0.4504\)

c)

	Jahr 1	Jahr 2	Jahr 3	Jahr 4
Ergebnis	105	99,75	102,7425	107,87
Zuwachs	5	-5,25	2,9925	5,1275

Durchschnitt: 2,0925

Wachstumsrate: \(g = \Big(\frac{107,87}{100} \Big)^{1/4} - 1=0.01911\) = 1,91%

Gesamtwachstum: 7,87%

d)

1. 111,

e)

\(y_T = y_0 * (1+g)^T\)

1. 5500

2. 7320

3. 710214,66

4. \(Y_0 * e^g\) = 15020,83

f)

1. 0,2

2. 0,046

3. 0,0035

4. 0,18