15.12.2022 Gesamtwirtschaftliches Gleichgewicht in der kurzen Frist

Konjunkturphasen

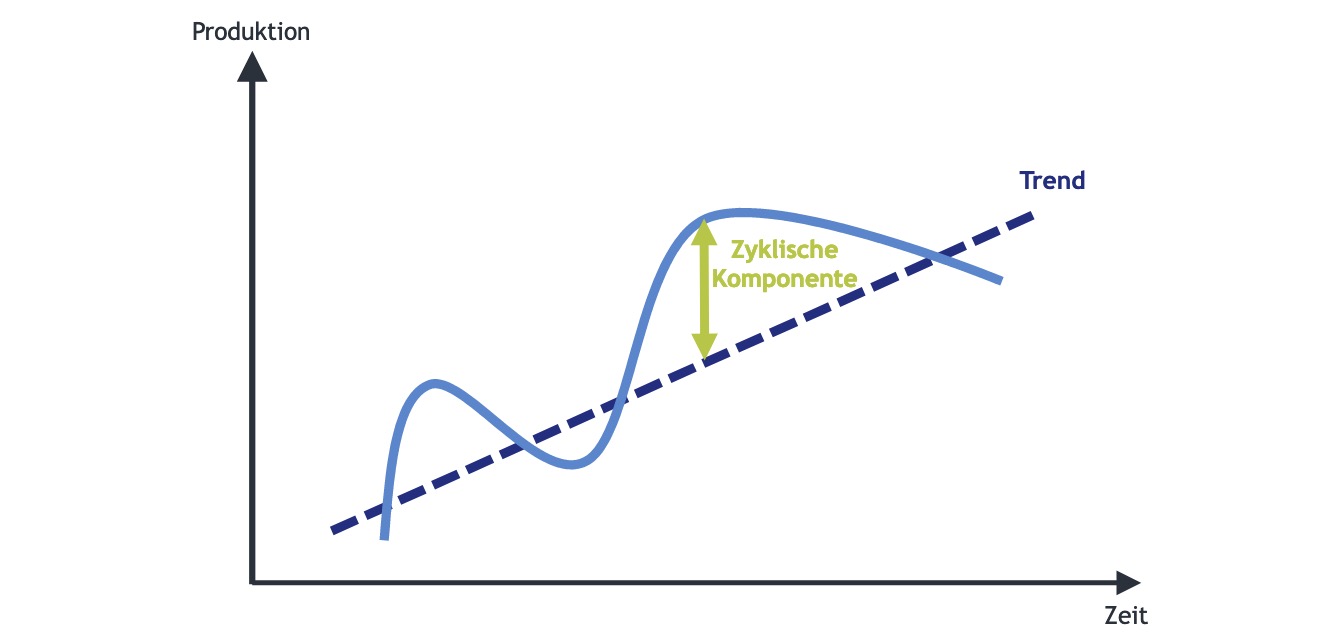
vorher: Trend, jetzt Zyklus

• 2 Phasenschema: Aufschwung (Boom); Abschwung (Rezession)

• 4 Phasenschema:

  • steigende Auslastung / sinkende Auslastung

  • Überauslastung / Unterauslastung

	Überauslastung	Unterauslastung
steigende A.	Boom	Erholung
sinkende A.	Abkühlung	Krise

stylisiertes Schema: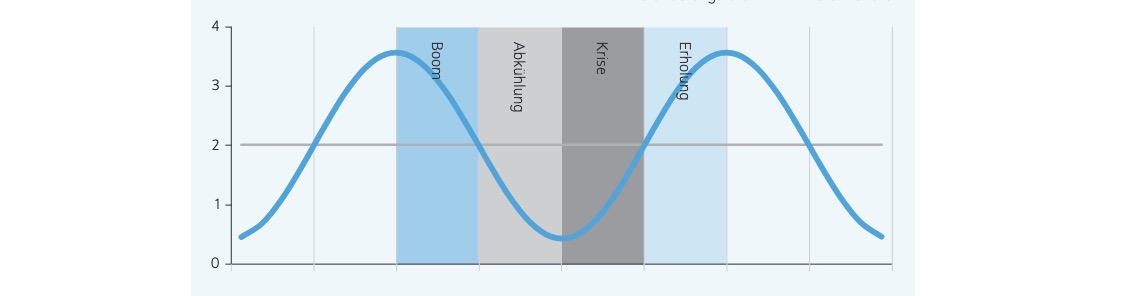

Verwendungsrechnung

Methode der BIP-Berechnung

  Private Konsumausgaben   C
+ Staatsausgaben           G
------------------------
= Konsumausgaben
+ Bruttoinvestitionen      I
+ Exporte                  X
- Importe                  Z
========================
= BIP                      Y

Y = C + G + I + X - Z

Wachstumsbeitrag

Anteil der Unterkategorien am Wachstum des BIPs

Berechnung: $\( Y = \frac{\Delta Y}{Y_{t-1}} = \frac{\Delta y_1}{Y_{t-1}} +\frac{\Delta y_2}{Y_{t-1}} \)$ Beiträge in DE

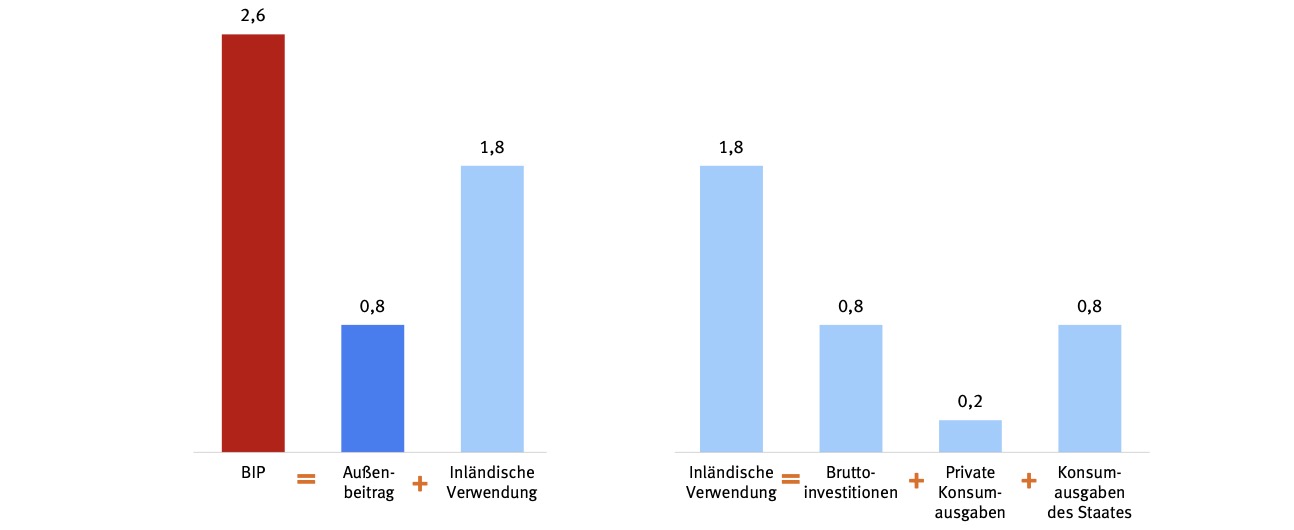
wichtige Gleichungen

1. Verwendungsidentität: \(Y = C + G + I + X - Z\)

2. Konsum: \(Y = C+S+T\) (Consum, Savings, Taxes)

Gleichsetzen von 1 und 2 und Kürzen C: $\( (S-I)+(T+G) = \underbrace{(X-Z)}_{\text{Handelsbilanz}} \)$

• geschlossene Wirtschaft: Staatliche Mehrausgaben = Ersparnissüberhang

• offene Wirtschaft: staatliche Mehrausgaben = Verschuldung Ausland erhöhen

Keynesianisches Modell

Keynes an sich ist so ein Banger, aber sein Modell nervt

Annahme: Güterpreise kurzfristig starr

• Konsumfunktion: \(C = C(\Omega, Y-T)\)

  • Vermögen \(\Omega\)

  • BIP = Y

  • Steuern T

• Investitionsfunktion \(I = I(\overset{-}{R},\overset{+}{A})\)

  • R = Realzins

  • A = Produktivität

• Staatsausgaben = exogen, unabhängig von Konjunktur

• Importfunktion \(Z=Z(\overset{+}{Y},\overset{+}{\sigma})\) (Wechselkurs)

• Exportfunktion: \(X = X(\overset{+}{Y},\overset{-}{\sigma})\)

• Handelsbilanz: \(TB = TB(\overset{-}{Y},\overset{+}{Y^*}, \overset{-}{\sigma})\)

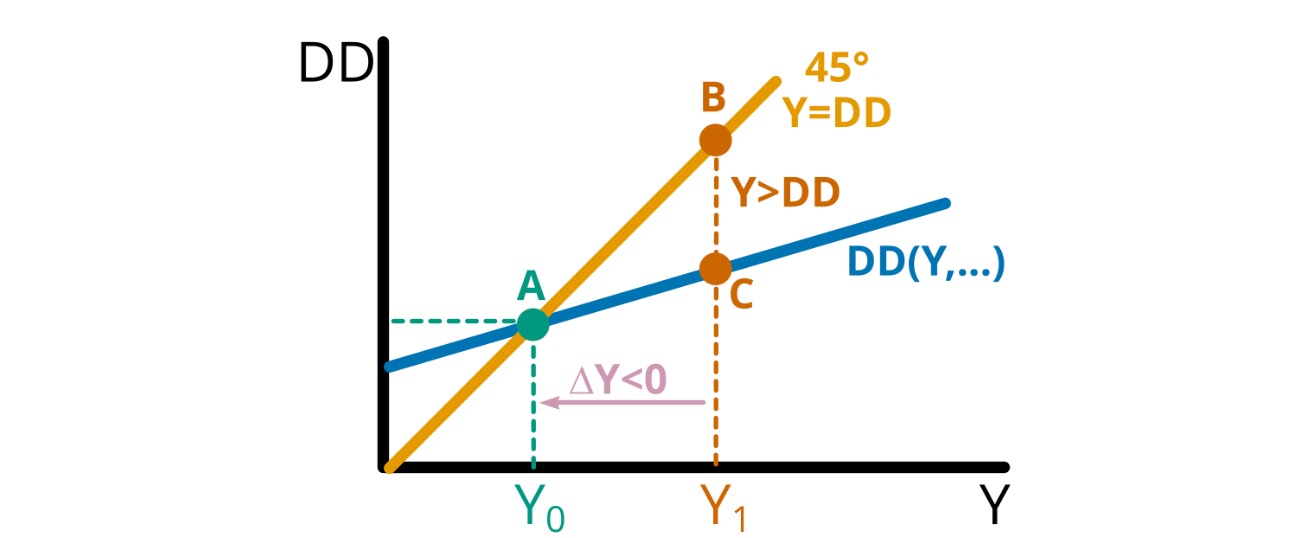
Keynesianisches Modell = nachfrageorientiert $\( DD = C()+I()+\bar{G}+TB() \)$

• Unternehmen passen sich an Nachfrage an

• Ausgaben abhängig von Einkommen, aber unterproportional:

  • zusätzliches Einkommen teilweise gespart und

  • für Importe ausgegen

• Gleichgewicht in A (immer mit 45% Linie)

komparative Statik: Anstieg der Staatsausgaben

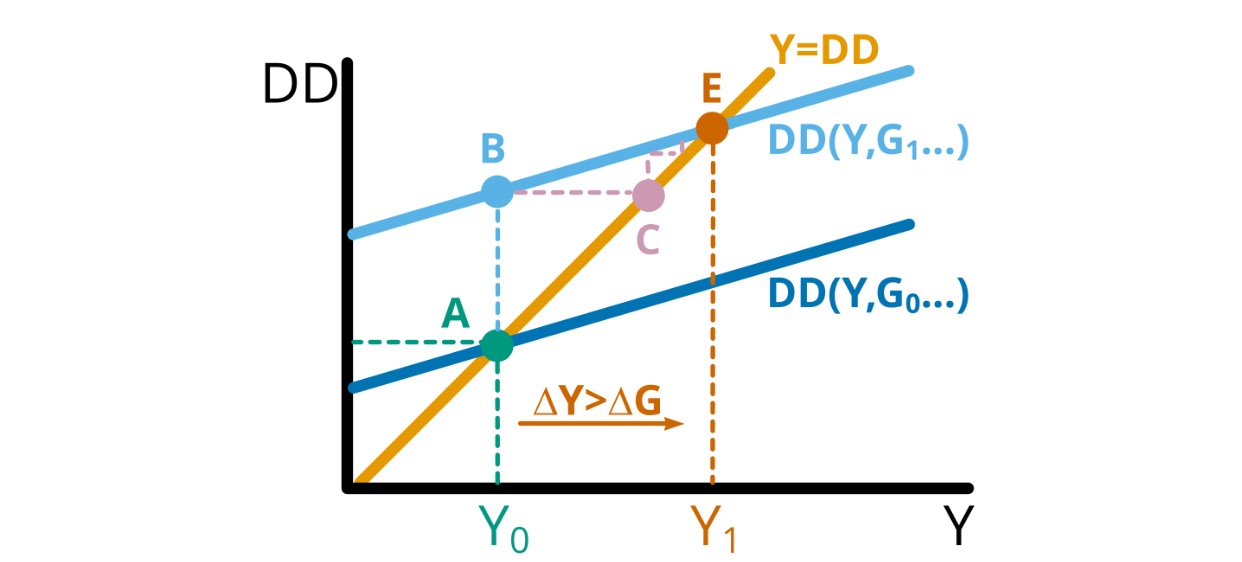
• Kurve DD verschiebt nach oben

• Angebot passt sich an

• um mehr als Anstieg der Staatsausgaben, da diese zurückverwendet werden

  • Multiplikatoreffekt \(\Delta Y > \Delta G\)

IS-LM Modell

analytische Modellierung von Keynes General Theory

• Anpassung von Modell an Inflationäre Wirkung

• Betrachtung von Geldmarkt und Gütermarkt

• bestimmt #klausurrelevant

IS-Kurve = Geldmarkt

mögliche Kombinationen von Zinssätzen und realen Marktoutput

• Annahme: I=S, Investittionen = Ersparnisse

  • höhere Zinssätze = weniger Investitionen = weniger Nachfrage

• Ableitung der Nachfrage nach Zinssatz

  • IS-Kuve = abhängig von Zinsreagibilität der Nachfrage

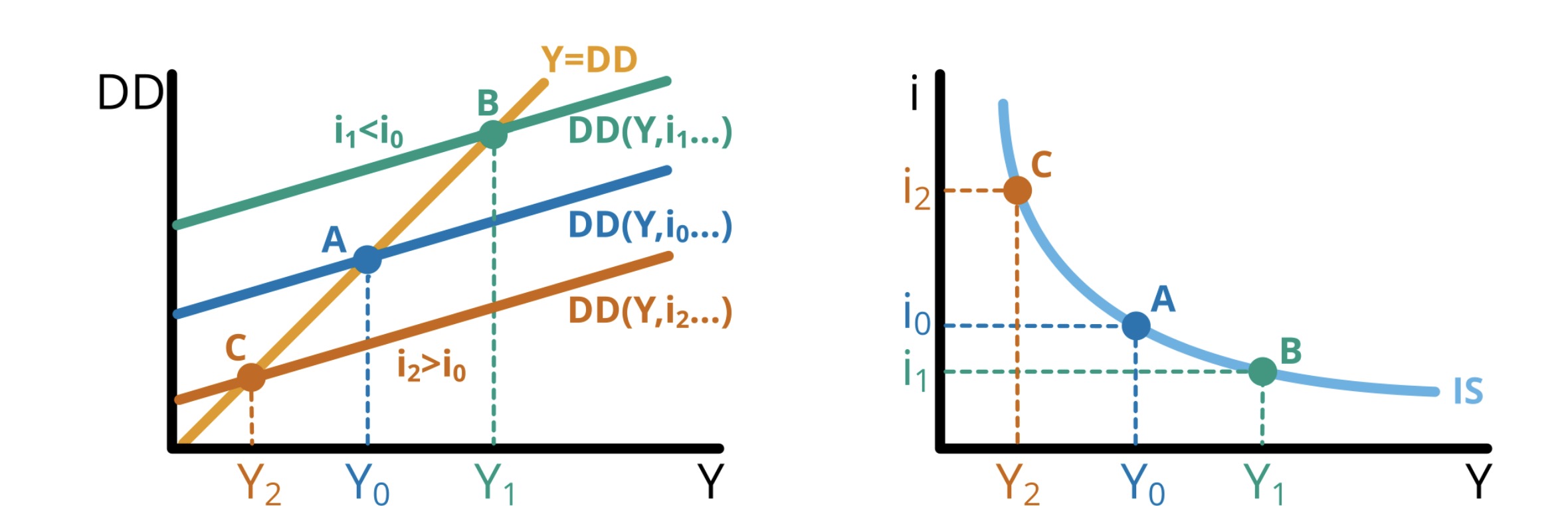
• Niedriger Zins = bessere Wirtschaft

• ohne Inflation: \(\pi = 0 \to\) i=R

Alternativ: exogene Erhöhung der Nachfrage

= keine Zinswirkung!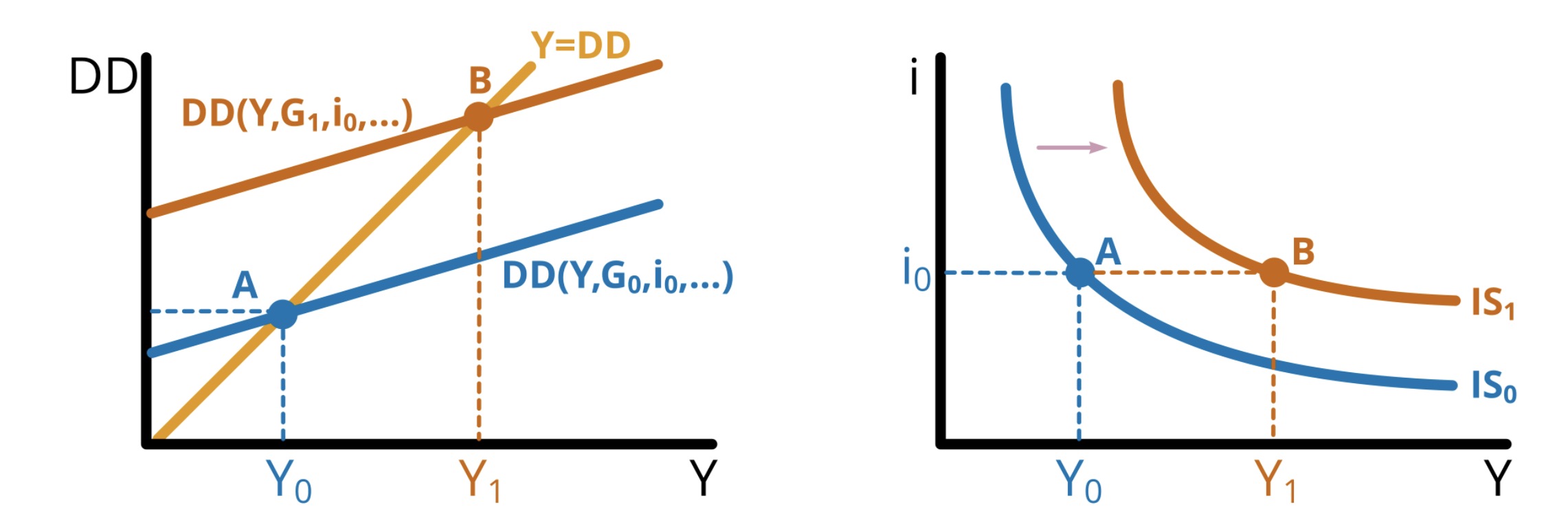

MP = Monetary Policy

die Zentralbank setzt den Marktzins = Monetäre Politik

nach John Taylor (1993)

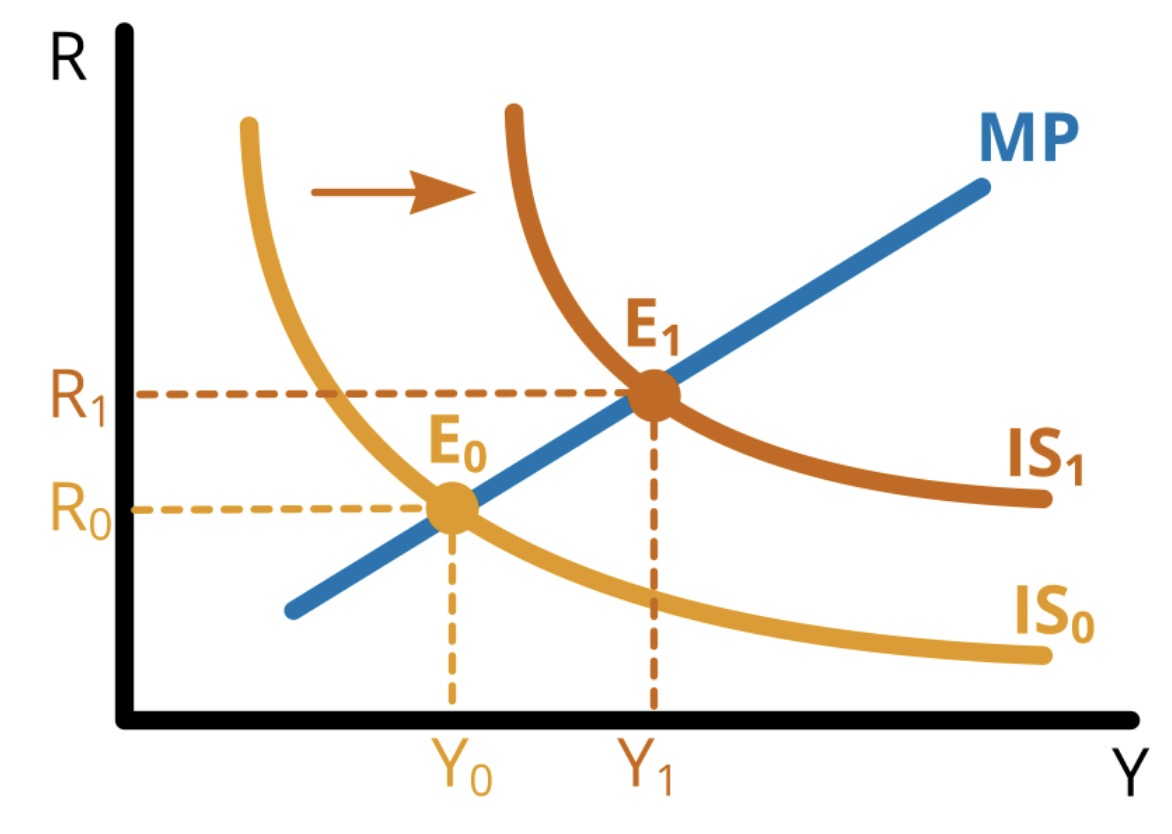
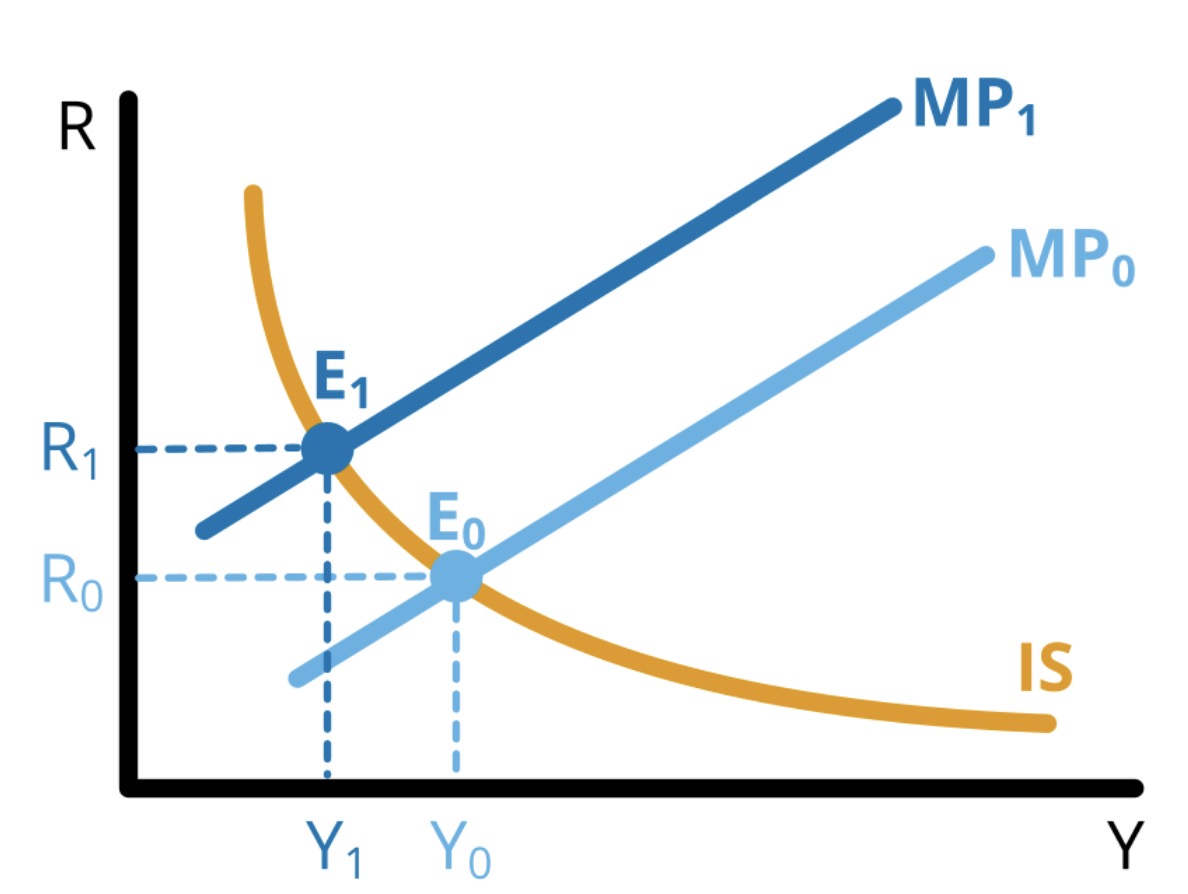
IS-MP

Treffpunkt beider Kurven

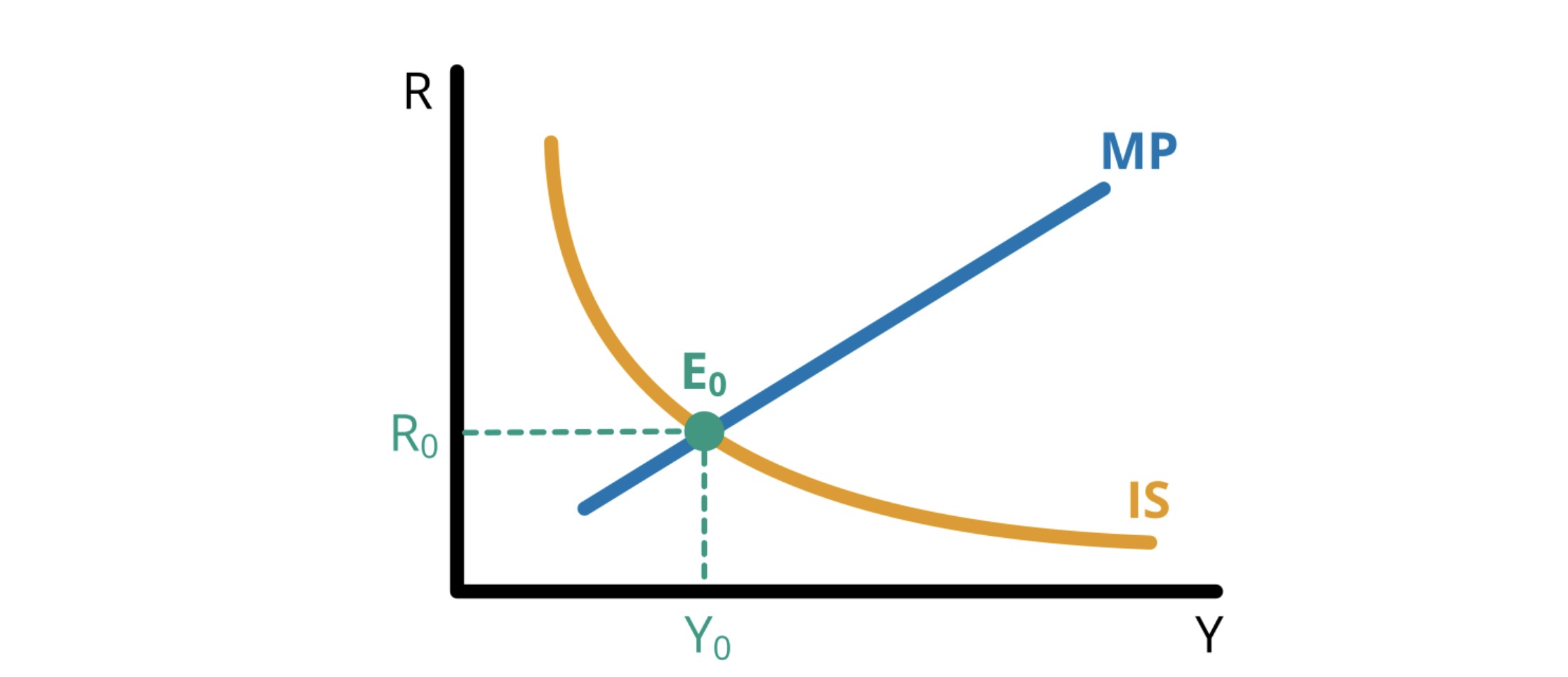
Instrumente des Staates:

• Fiskalpolitik (restriktiv / expansiv)

• Geldpolitik (retstrikitv / expansiv)

expansive Fiskalpolitik	restritkive Geldpolitik

durch Zusammenspiel beider Politik lässt sich jeder Punkt in Graph erreichen!

Geldmarkt & Zinspolitik

Übung

Aufgabe Ausgabenmultiplikator

• Konsumfunktion: \(C = \bar{C}+cY = \bar{C}+(1-s)Y\)

• Agg. Nachfrage: \(\bar{G} + \bar{I}+\bar{TB} + C= \bar{DD} +cY\)

Angebot = Nachfrage

• Gütermarkt GG: \(Y = \bar{DD}+cY\)

• nach Y: \((1-c)Y = \bar{DD} \to Y_0 \frac{1}{(1-c)}\bar{DD} \)

• Ausgabenmultipliaktor: \(\Delta Y = \frac{1}{(1-c)}\Delta \bar{DD} = \frac{1}{s}\Delta \bar{DD}\)

  • bei Sparquote von 0,2:

  • Anstieg Staatsausgaben um 1 Einheit

  • = Anstieg Y um 5