17.01.2022 Transportoptimierung

Transportprobleme: besondere Art von Linearen Optimierungsproblemen mit gleichen Voraussetzungen

Eigenschaften

• Kunde $j$ will Menge $b_j$

• Lieferant $i$ kann Menge $a_i$ liefern

• $c_{ij}$ = Kosten des Transports von Lieferant $i$ an Kunde $j$

• Kunde kann mehrere Lieferanten haben, Lieferant mehrere Kunden

Suche: Transportmenge $x_{ij}$ für Transport $i\to j$ mit minimalen Kosten

Beispiel 155:

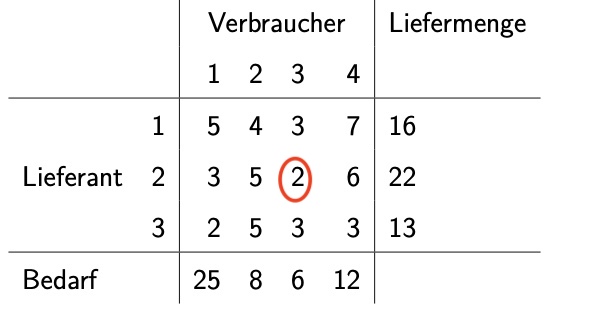
Beispiel: Lieferkosten $c_{23}$ für Lieferant 2 an Verbraucher 3 pro Einheit: 2

Voraussetzung: Gesamtbedarf = Gesamtliefermenge = 51 (dieses Beispiel) = ausgeglichen

• sonst zusätzliche Kunden / Lieferanten, die kostenlos abnehmen

! Transportproblem ist immer lösbar !

ist eigentlich Simplexverfahren, aber ohne Umformung in St. Max. Problem

zulässige Basislösung bestimmen

• Kostenmatrix des TP: $C=(c_{ij})\in {\mathbb{R}}^{n,m}$

• Mengenmatrix des TP: $X=(x_{ij})\in {\mathbb{R}}^{n,m}$

Menge an Basisvariablen = $m+n-1$ = hier 6

• Basisvariable = Ergebnisse in der Mengenmatrix verschieden 0

• wenn mehr: irgendwas falsch

• wenn weniger: ausgeartet

mithilfe der Nordwesteckenregel: von oben links versuchen maximale Liefermengen einzusetzen

Ergebnis: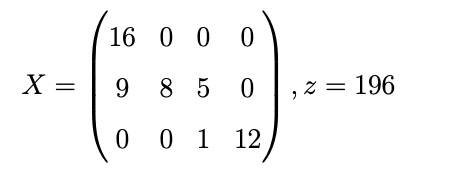

merke:

• die Matrix hat 6 Einträge verschieden 0 = Basisvariablen

• Kosten z = X*C

oder mithilfe der Methode des Matrixminimum

Anfangslösung verbessern

• Bestimmung der Variablen, die in die Basislösung getauscht werden : Potentiale

• Art des Tauschs: Austauschkreis