25.04.2022 Stichproben#

Unabhängigkeit#

zweier Ereignisse

Definition: \(P(A \cap B) = P(A) * P(B)\)

Beispiel: Wahrscheinlichkeit beim Würfeln für zwei Sechsen : \(\frac{1}{6}*\frac{1}{6}=\frac{1}{36}\)

Zufallsstichproben#

wenn Ergebnissmenge eines Experiments nicht bekannt => Stichproben

  • aus Stichproben Wahrscheinlichkeit ablesen

  • Wahrscheinlichkeit für Objekt in Grundgesamtheit benötigt

Fakultät#

k! = 1*2*...*(k-1)*k
0! = 1

Binomialkoeffizient#

m über k: \(\binom{m}{k} = \frac{m!}{k!*(m-k)} , k \le m\),

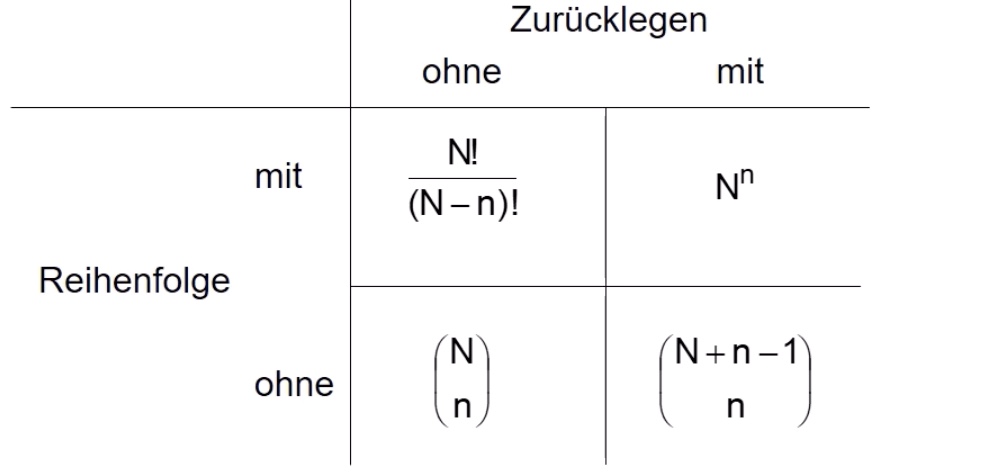
Ziehungsmodelle#

  • ohne / mit Zurücklegen

  • ohne / mit Beachtung Reihenfolge

Grundgesamtheit N, Stichprobengröße n

2022-04-24_10.22.13

Geburtstagsproblem mit 23 Gästen

  • Gegenereignisse, dass alle an unterschiedl. Tagen Geburtstag haben:

    • \(\frac{N!}{(N-n)!} =\frac{365!}{(365-23)!}= 4.22 * 10^{58}\)

  • alle möglichen Kombinationen:

    • \(N^n = 365^{23} = 8.56 * 10^{58}\)

  • Laplace Wahrscheinlichkeit, dass alle an unterschiedlichen Tagen GB

    • \(\frac{4.22}{8.56} = 0.49\)

  • Gegenwahrscheinlichkeit dass es gleiche Geburtstage gibt

    • \(1- 0.49 = 0.51\)

ab 23 Personen lohnt die Wette!

Zufallsvariablen#

Aus Vorlesungsteilnehmern eine Person auswählen

  • Ergebnismenge \(|\Omega| = N\)

  • \(P(\{ \omega \} ) = \frac{1}{N}, \forall \omega \in \Omega\)

Interesse an Merkmalen (Zufallsvariablen) der Person

  • Beispiel Alter X Abbildung auf Grundgesamtheit: \(X : \Omega \to \mathbb{R}, \omega \to X(\omega)\)

  • kann diskret oder stetig sein

Verteilungsfunktion und Dichte#

  • Verteilungsfunktion = empirische Verteilungsfunktion aus Stat. I

  • Dichte = relative Häufigkeitsverteilung

  • diskrete Dichte = Wahrscheinlichkeit

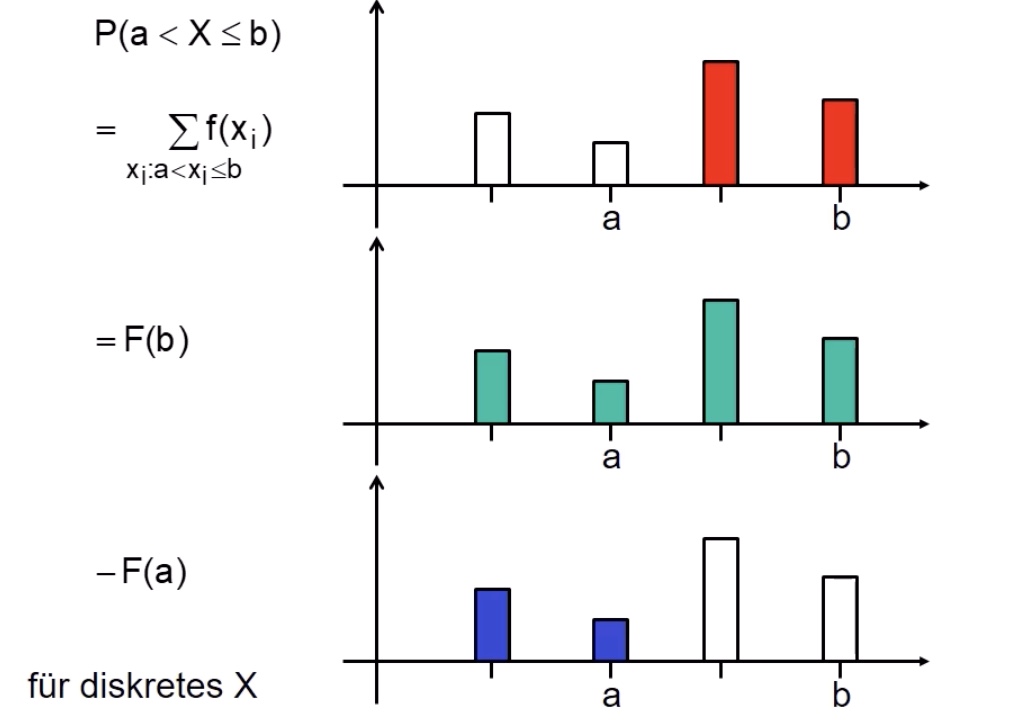
Dichte: \(P(X \le x) = \sum_{x_i \le x} f(x_i)\)

2022-04-24_12.38.38

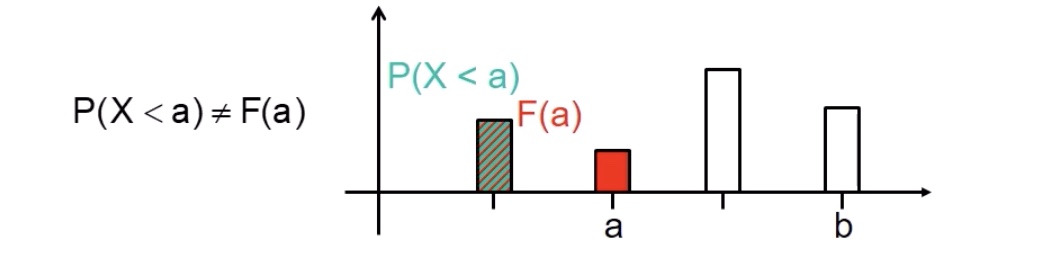
Wichtig: \(P(X< a) \neq F(a)\)

2022-04-24_12.40.02

Beispiel Würfeln#

  • X = Augenzahl

  • \(X(\Omega) = \{x_1,...,x_6 \} \)

  • \(P(X = x_i) = 1/6\)

  • diskrete Dichte: \(f(x_i) = 1/6, i= 1,...,6\)

Verteilunsfunktion

\(x_i\)

1

2

3

4

5

6

\(f(x_1)\)

1/6

1/6

1/6

1/6

1/6

1/6

\(F(x_i)\)

1/6

2/6

1/2

4/6

5/6

1

Wahrscheinlichkeit für Zahl X zwischen 2 und 6 $\( \begin{aligned} &\to P(2 < X \le 5) \\ &=P(X \le 5) - P(X \le 2) \\ &= F(5) - F(2) \\ &= 5/6 - 2/6 = 1/2 \end{aligned} \)$