17.01.2023 Klima-Solow Modell#

  • IPAT-Modell: keine Rückwirkungen der Umweltschäden auf Wachstum

=> Klima-Modelle

  • CO2 = globale Externalität

    • Auswirkungen unabhängig von Emissionsort

    • Schäden nicht immer an Ort der Emission

Klima-Solow#

Herausforderungen der Klimamodellierung:

  • Kosten / Nutzen von Klimaschutz unterschiedlich verteilt

    • intra-generational equity: Asugleich zw. heute lebenden Armen / Reichen

    • inter-generational equity: heutige Emission = Bürde für nachkommende

  • CO2 = Tragedy of the Unmanaged Commons

    • einzelne beste Handlungsoption \(\neq\) gemeinschaftliche beste

    • Kosten einer Handlung werden auf alle verteilt

    • => Anreiz zur Übernutzung

Klimaschutz = öffentliches Gut (Vorteile nicht rivalisierend)

Klima-Solow = vereinfachtes Integrated-Assesment-Modell (IAM) nach Tsigaris & Wood (2016)

  • Produktionsfunktion mit Emissionen

  • Temperaturen

  • Rückkopplung der Temperaturen auf Produktion

graph LR W(Wachstum) --mehr--> E(Emissionen) --mehr--> T(Temperaturanstieg) S(Schaden) Population & Technologie & Einkommen -.-> W T --mehr--> S S --weniger--> W

Produktionsfunktion#

jetzt mit Schadensfunktion: $\( y = D_t \cdot A_t \cdot k^a_t \\ \)\( mit \)\( D_t = \frac{1}{1+\theta_1 \cdot Temp_t^{\theta_2}} \le 1 \)$

Wobei \(Temp_t\) = Temperatur-Anomalie und \(\theta_{1,2}\) = positiv

  • je größer Temperaturanomalie = kleiner D

  • => kleiner y = großer Schaden

Beispiel mit 0, 1, 4 Grad und \(\theta_1 = 0.002384; \theta_2 = 2\)

  • Temp = 0: \(D = \frac{1}{1+0.002384 \cdot 0^2} = 1\)

  • Temp = 1: \(D = \frac{1}{1+0.002384 \cdot 1^2} = 0.99 \)

  • Temp = 4: \(D = \frac{1}{1+0.002384 \cdot 4^2} = 0.96\)

Bevölkerung und Technik#

  • Sparquote s und Abschreibung \(\delta\) wie gewohnt

  • Bevölkerungswachstum n modelliert als abnehmend (mit \(\delta\)) wegen langfristigkeit

\[ n_t = \frac{n_0}{(1+\delta_n)^t} \]

  • technologischer Fortschritt g ähnlich

\[ g_t = \frac{g_0}{(1+\delta_g)^t} \]

Auflösung#

ausgewogener Wachstumspfad: $\( k^* = \Big( \frac{s \cdot D_t \cdot A_t}{n_t+\delta}\Big)^{\frac{1}{(1-a)}} \)$ Wachstumsrate hängt ab von Damage-Function, abnehmende g und Wachstum von a

img

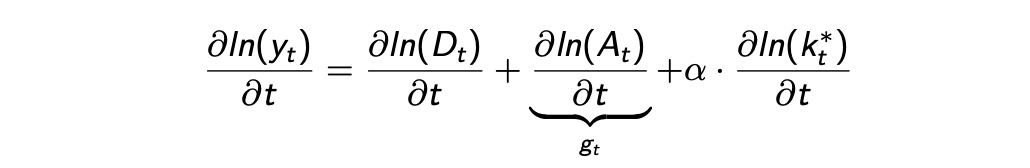
Beispielmodellierung:

img

Emissionen#

  • Produktion sorgt für Emission

\[ E_t = \sigma_t \cdot Y_t \]

abhängig von Emissionsintensität \(\sigma\) (ähnlich zu Technologie aus IPAT) $\( \sigma = \sigma_{t-1} \cdot (1+g_\sigma) \text{ mit } g_\sigma < 0 \)$

  • die Emissionsintensität sinkt jedes Jahr

  • \(g_\sigma \neq\) technischer Fortschritt!, sondern anderer Parameter

Emissionen und Jahr / Einkommen

img

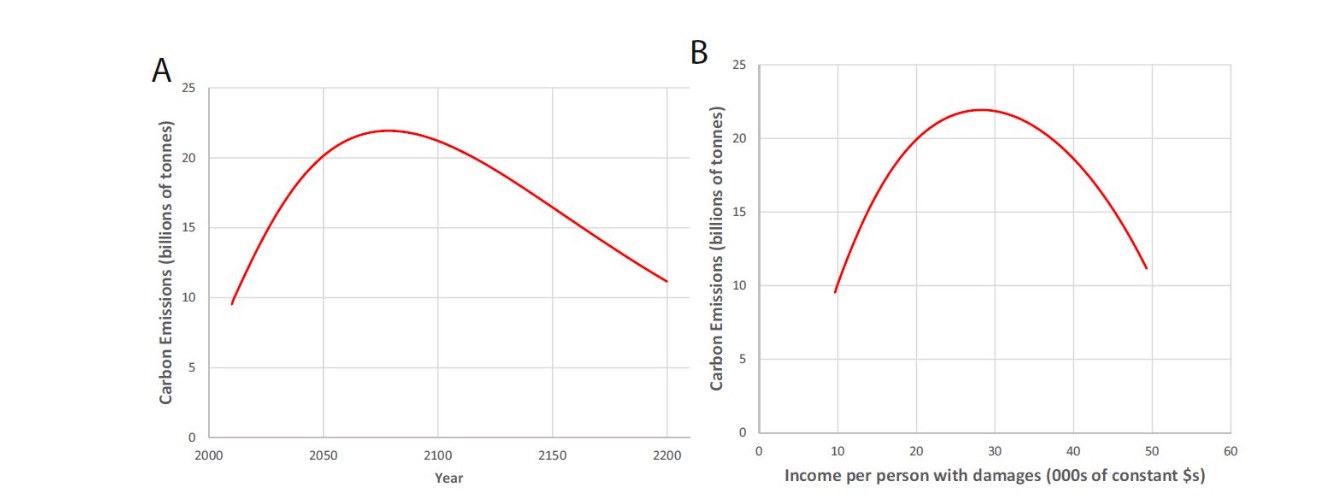
Wachstum der Emissionen wie IPAT: $\( g_{E,t} = n_t + g_{y} + g_{\sigma} \)$

  • bis 2075: keine Senkung, da \(n+g_y>g_\sigma\)

    • absolut wachsende Emissionen

  • Danach bessere Damage-Function und mehr Umweltschäden

    • absolut sinkende Emissionen

Temperatur#

Zusammenhang zw. Emissionen und Temperaturanstieg

  • 1000 Mrd. Tonnen CO2 = 1.8° Erwärmung

  • proportionale Beziehung, abhängig von Ausgangs-CO2 C

\[ Temp_t = \beta \cdot (C_0+\sum_1^t E_t) \]

um auf 2° zu begrenzen, begrenze Neuemissionen möglich

Grenzen des Wachstums#

„The Limits to Growth“

  • von Meadows, Randers Behrens

  • 1972 vom Club of Rome

Simulation der natürlichen Grenzen basierend auf Ressourcen

5 Variablen:

  1. Bevölkerungsentwicklung

  2. Nahrungsmittelerzeugung

  3. Industrieproduktion

  4. Umweltverschmutzung

  5. Verbrauch nicht-erneuerbarer Ressourcen

Annahmen: exponentielle von allem außer Innovation (linear)

Ergebnisse: 2 Szenarien

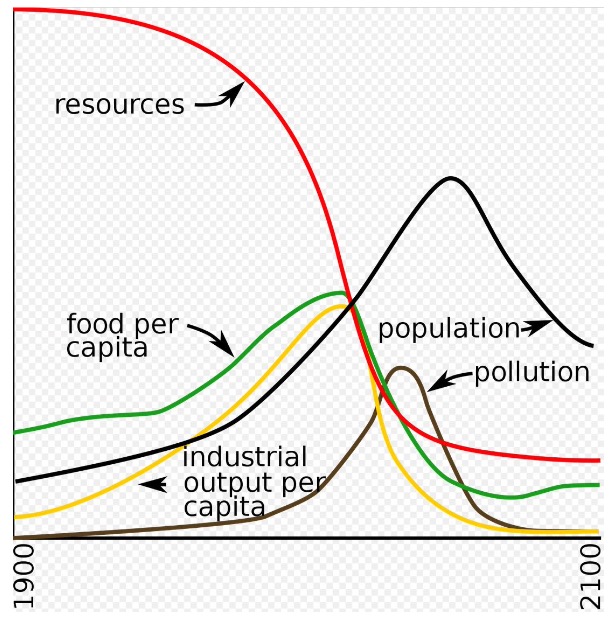
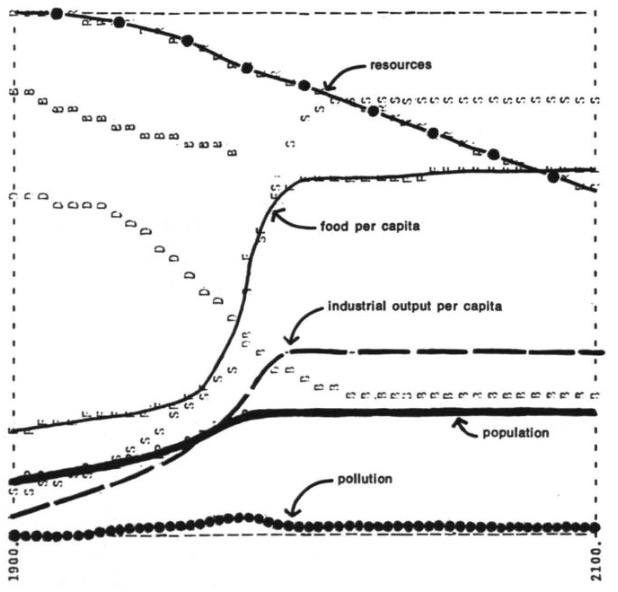
Overshoot and Collapse Szenario

Stabilisierungszenario

2023-01-17_11-23-49

img

  • im ersten: nichts mehr zu essen, und dann Sterben und Zusammenbruch

  • Stabiliserung: genug für alle, braucht:

    • Rückgang des Bevölkerunswachstums (teilweise eingetreten)

    • Strukturwandel zu Dienstleistungen (eingetreten)

    • Stabilisierung des Kapitalstocks (nicht eingetreten)

    • Reduzierung der Umweltverschmutzung pro Einheit (nicht eingetreten)

Diskussion:

  • Ökonomen: zu wenig technischer Fortschritt

  • Unternehmen: Einschränkung der freien Wirtschaft

  • Linke: Einschränkung Wachstum = Verhinderung höheres Lebenstandards

aber:

  • erste Diskussion des globalen Ressourcenverbrauchs

  • stark abhängig von Szenarien

  • manche Vorhersagen nciht akkurat (Öl)

Postwachstum und Degrowth#

Wie weiter mit dem Wachstum?

mehr Reichtum fördert nicht Lebenszufriedenheit (in Reichen Ländern)

Konzepte:

  • Wachstumsgrenzen

  • Wachstumszwänge

  • alternative Wohlfahrtsmaße

  • Strukturwandel

Fragen:

  • wer darf noch wachsen?

  • individuell oder politisch einschränken?

Green Growth#

Lösung des Konflikts zwischen Wachstum und Ökologie

  • langfristiges Wachstum

  • Entkopplung von Emission und Produktion

  • Wachstum von energieschonenden Technologien

    • verbesserte Effizienz

  • Kreislaufwirtschaft & Recycling

  • Vermeidung des Rebound-Effekts