02.06.2022 Normalverteilung 2#

Quantile der Normalverteilung#

bereits bekannt aus Statistik I

Suchen das 99% Quantil der Standardnomalverteilung

Berechnung mit R

q = 0.99 # der gesuchte Wert
m = 0 # Mittelwert mu der Verteilung
sd = 1 # die Standardabweichung
# Berechnung der Wahrscheinlichkeit mit pnorm()
qnorm(p,m,sd)

Output

2.326348

also ist 2.32 der Wert auf der Skala, an dem 99% der Verteilung inbegriffen sind

anders Beispiel:

q = 0.691 # der gesuchte Wert
m = 5 # das mu der Verteilung
sd = 2 # die Standardabweichung
# Berechnung der Wahrscheinlichkeit mit pnorm()
pnorm(q,m,sd) 
# => 5.999

Darstellung: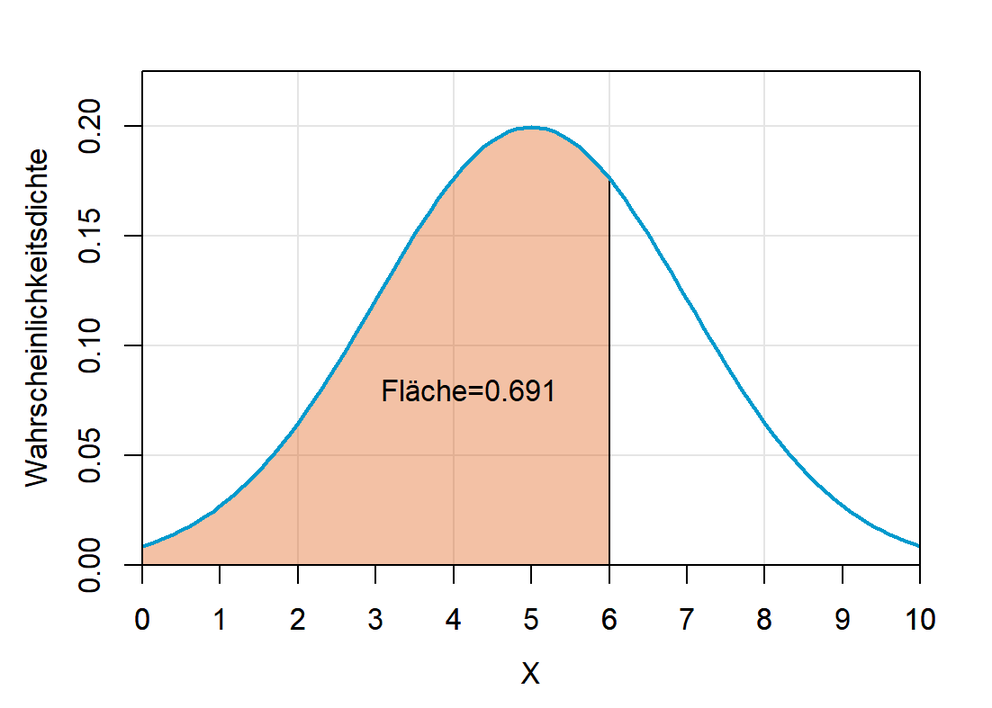2022-06-02_12-39

qnorm() ist das Gegenteil von pnorm()!

Beispiel#

Produzierendes Unternehmen braucht Lager => perfekte Dimensionierung?

  • Gegeben:

    • Durchschnittlich benötigte Lagerfläche: 120

    • Variabilität der genutzen Fläche: 400

  • Gesucht:

    • Lagerfläche X

Modellierung mithilfe von Normalverteilung: \(X \sim N \ (120,400)\)

  • dann mithilfe der gewünschten Sicherheit Lagergröße bestimmen

  • wir wollen 80% der Lagerzustände abdecken

  • qnorm(0.8,m=120, sd=400) => 456.6485 Quadratmeter sind dafür passende Fläche

Schätzer#

Modell: vereinfachte Darstellung der Geschehnisse der Wirklichkeit

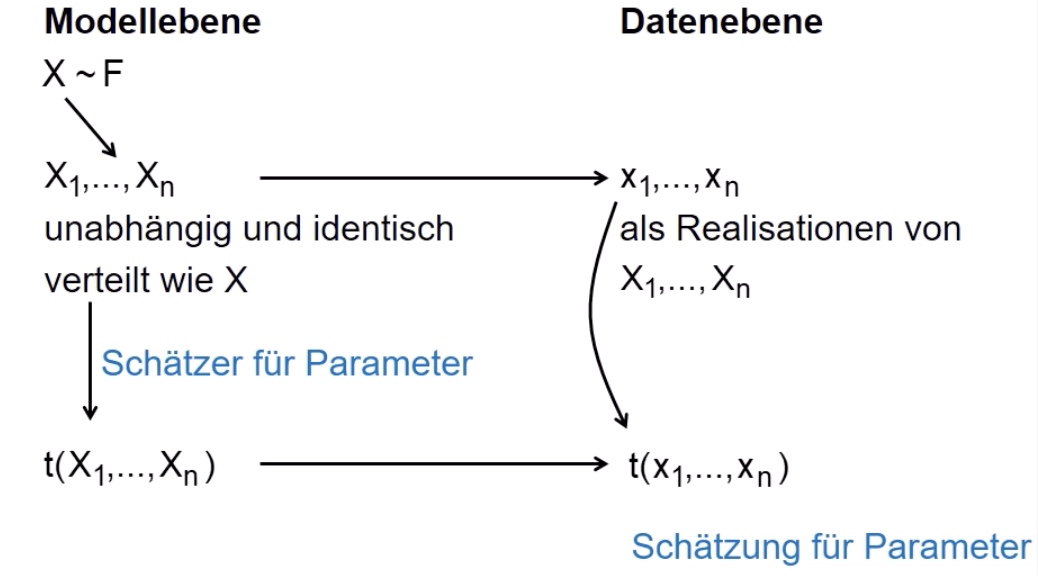
2022-06-02_13.06.43

beachte Unterschied zwischen Schätzer und Schätzung!