16.11.2021 weitere Lagemaße#
Median#
Median: Mitte einer geordneten Beobachtungsreihe
wenn n ungerade: \(x_{med}= x_{ \left( \frac {n+1} {2} \right) }\)= Mittlere Zahl
wenn n gerade: \(x_{med} = \frac{1}{2} * \left( x_{\left( \frac {n} {2} \right)} + x_{\left( \frac {n+1} {2} \right)} \right)\) = Mittelwert der mittleren Zahlen
Modus#
Modus: Merkmal mit größter Häufigkeit \(x_{mod}\)
wie viele Merkmale von Modus gibt es = Modalitätsgrad
Modalitätsgrad = \(h(x_{mod}) / n\) relative Häufigkeit des Modus
Sonderfälle#
Transformationen#
Transformation von Lagemaßen bei linearen Transformationen möglich: \(y_i = a*x_i + b \iff \bar{y} = a * \bar{x} + b\)
Klassierte Daten#
Lagemaße wie arithmetisches Mittel nur näherungsweise berechenbar
Vorgehen:
für jede Klasse Klassenmitte m bilden
m gewichten mit mit häufigkeit f
Durchschnitt aller Klassen bilden
Notation: \(\bar{x}_{klass} = \sum_{j=1}^k m_j * f_j\)
Quantile#
Aufteilung der Beobachtung in Werte unter-/ oberhalb von \(x_p\)
p-Quantil: \(x_p\) teilt Beobachtungsreihe auf in zwei Anteile

für 0 < p < 1;
falls n*p nicht ganzzahlig = aufrunden
Studiendauer: n = 36, p = 0,9
n * p = 36 * 0.9 = 32.4 -> aufrunden auf 33
=> 33ten Wert aus geordneter Reihe ablesen
Ergebnis: \(x_{(0.9)} = x_{(33)} \)
falls n*p ganzzahlig = Mittelwert von \(n*p \) und \( n*p+1 \)
Studiendauer, n = 36, p = 0.75
n*p = 27 -> ganzzahlig
=> Mittelwert aus 27ten und 28ten Wert
Ergebnis: \(x_{(0.75)} = \frac{1}{2}* (x_{(27)} + x_{(28)} )\)
Spezielle Quantile#
p = 0.25 : 1. Quartil
p = 0.5 = Median, 2. Quartil
p = 0.75 : 3. Quartil
Fünf-Punkte-Zusammenfassung#
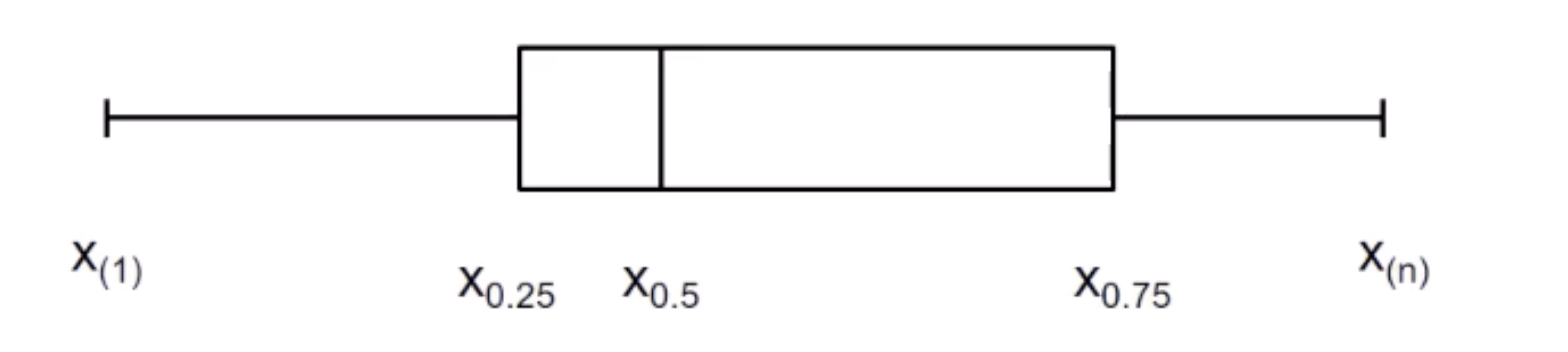
Beobachtungen unterteilt in 4 Intervalle durch 5 Schnitte
\(x_{(1)}\) = Minimum
1. Quartil
Median
3. Quartil
\(x_{(n)}\) = Maximum
Graphische Darstellung mithilfe des Boxplots