17.05.2022 Verteilungen

Bernoulli Verteilung

binäre Verteilung als 0 oder 1

• bspw. Klausur bestanden / nicht bestanden mit Wahrscheinlichkeit p

Dichtefunktion: \(f(x_i) = p^{x_i} * (1-p)^{1-x_i}\) für \(x_i = 0,1\)

ist Spezialfall der Binomialverteilung: \(X \sim Bin(1,p)\)

Binomialverteilung

Dichtefunktion: $\( f(x_i) = \underbrace{\binom{n}{x_i}}_{\text{Binomkoeff}} * \underbrace{p^{x_i}}_{\text{Erfolge}} * \underbrace{(1-p)^{n-x_i}}_{\text{Misserfolge}} \)$ Binomkoeffizient beschreibt Anzahl aller möglichen Kombinationen

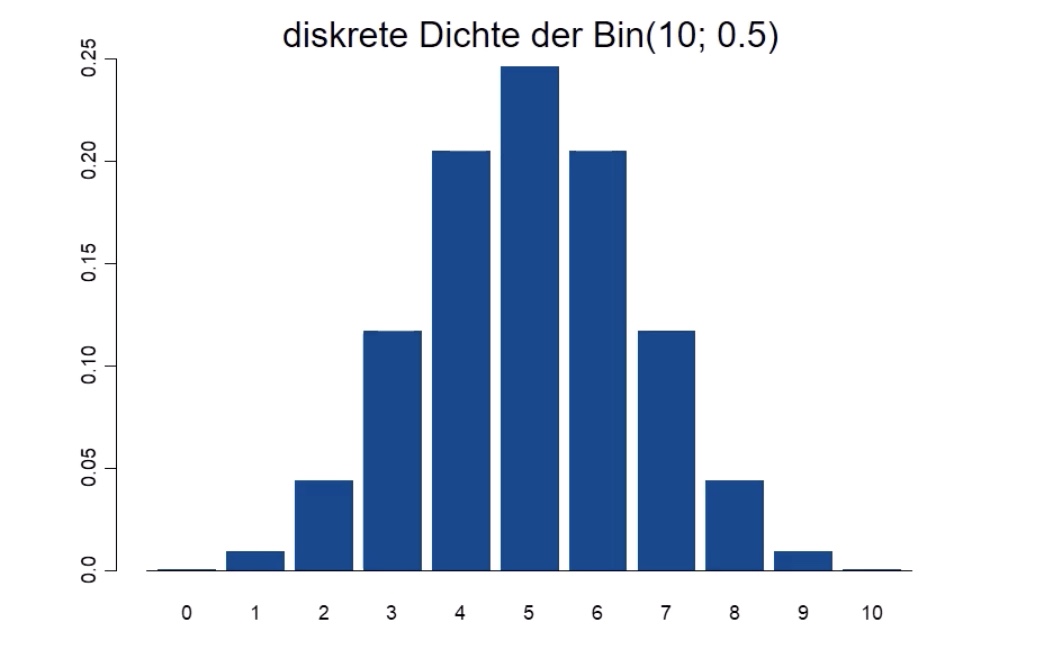
Binomialverteilung = Situation Ziehen mit Zurücklegen

• Urne mit N Kugeln, davon M mit interessierender Eigenschaft

• n Kugeln ziehen mit Zurücklegen

• \(X \sim Bin(n,p)\) mit \(p = M / N\)

hypergeometrische Verteilung

Ziehen ohne Zurücklegen

• Urne mit N Kugeln, davon M mit interessierender Eigenschaft

• n ziehen ohne zurücklegen

• \(X \sim Hyp(n,M,N)\)

Dichtefunktion: $\( f(x_i) = \frac{ \binom{M}{x_i} * \binom{N-M}{n-x_i} }{ \binom{N}{n}} \)$

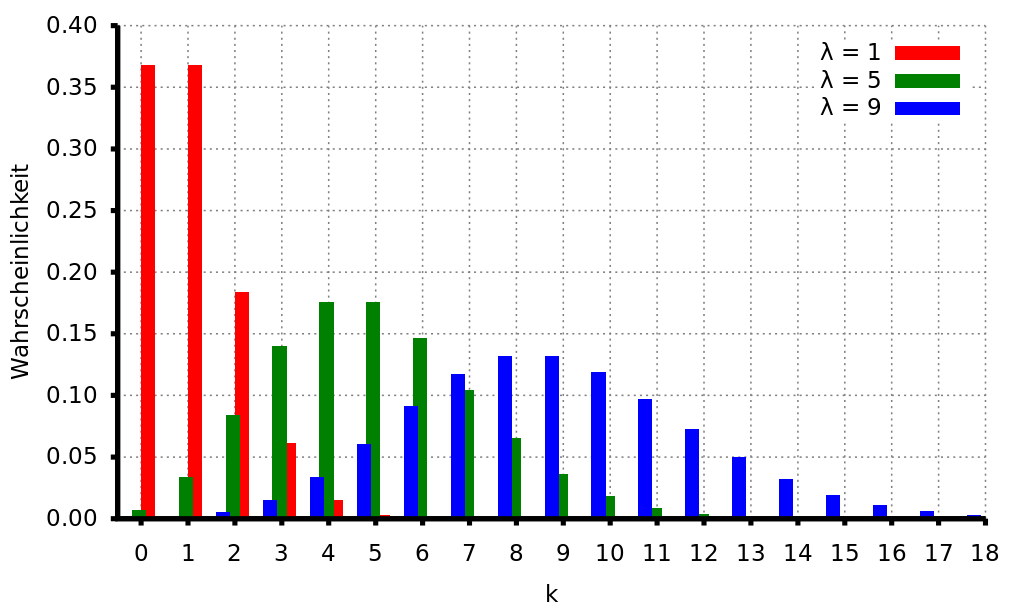
Poisson Verteilung

X diskrete Zufallsvariable: 0, 1, 2, …

Dichtefunktion: \(f(x_i) = \frac{\lambda^{x_i}}{x_i!} e^{-\lambda}\)

auch Verteilung der seltenen Ereignisse