18.10.21 erste Übung#

Wiederholung wichtiger Rechenregeln

Indizes#

bei einer Beobachtung (oft in Form einer Urliste): zu jeder Beobachtungseinheit liegt ein Wert vor

  • BSP: Person 1(Beobachtungseinheit Mensch) = 156cm (Wert der Körpergröße)

auch genannt Index und Variable $\( Beispiel \\ x_1 = 145cm \\ x_2 = 180cm \\ x_3 = 170cm \\ x_4 = 145cm \)$

Notation:#

  • Buchstabe i beschreibt Index

  • letzter Wert = \(x_n\)

  • wenn Variablen nach Größe geordnet => Indizes in Klammern mit dem letzten Wert als größten

    • \(Beispiel \\ x_{(1)} = 145cm \\ x_{(2)} = 145cm \\ x_{(3)} = 170cm \\ x_{(4)} = 180cm \)

Zusammenfassungen#

wenn Daten zusammengefasst werden (klassiert oder unglasiert)

=> Buchstabe j beschreibt dann den Index

Unklassierte Zusammenfassung: Werte werden getrennt in Wert und Häufigkeit des Auftauchens, dann ist \(a_j\) die Ausprägung und \(h_j\) die Häufigkeit

\(Beispiel \\ a_1 = 145 , h_1 = 2\\ a_2 = 180cm , h_2 =1 \\ a_3 = 170cm , h_3 = 3 \)

auch noch erweiterbar um relative Ausprägung \(f_i=f(a_i)=h(a_1)/n\)

Klassierte Zusammenfassung: Werte werden in Klassen (Bereiche) zusammengefasst

k = die Anzahl der Klassen, \(m_j\) die Klassenmitte und \(n_j\) die Anzahl an Beobachtungen in der Klasse

\(Beispiel (k=3) \\ Klasse 1: 130 < x ≤ 150 , m_1 = 140, n_1 = 2\\ Klasse 2: 150 < x ≤ 170 , m_2 = 160, n_2 = 1\\ Klasse 3: 170 < x ≤ 190 , m_3 = 180, n_3 = 1\)

Klassennotation:

  • mit [100-400] für einschließlich = 100-400

  • mit () für auschließlich = 101-399

  • BSP: [100,400) heißt hier einschließlich 100,…,399

Summenzeichen#

Bei Summierung vieler Messwerte => Summenzeichen \(\sum\)

\(\sum_{i=1}^n = x_1+x_2+...+x_n\)

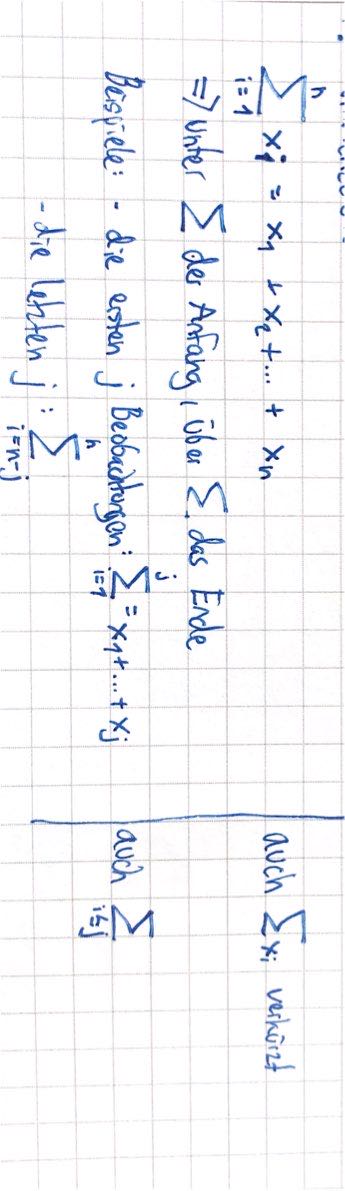
21-10-20_15-39-14

Regeln:

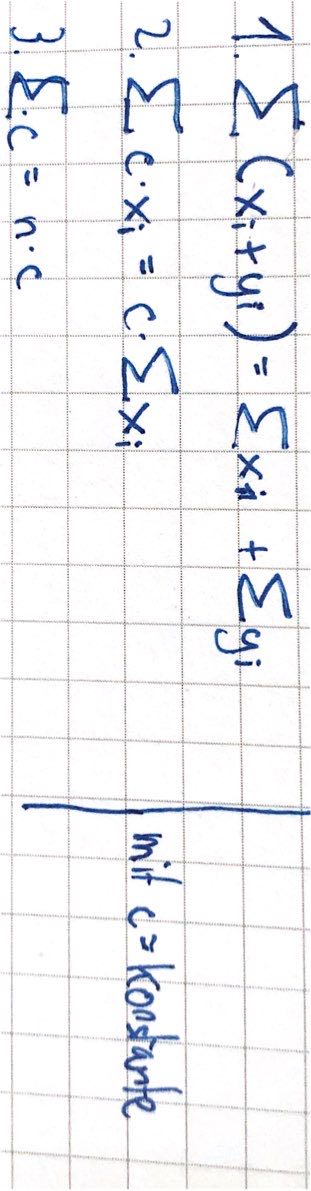
21-10-20_15-40-27

Produktzeichen#

funktioniert ähnlich wie Summenzeichen, nur halt multipliziert

\[\prod_{i=1}^n x_i = x_1 * x_2 * ... x_n\]

Logarithmus#

wenn \(a^x = b \) dann ist \( x = \log_a(b)\)

Sonderform natürlicher Logarithmus ln():

  • Basis ist e = Eulersche Zahl: \(e^x = b \implies x = \ln(b)\)

Rechenregeln:

\(ln(b*c) = ln(b) * ln(c) \\ ln(b/c) = ln(b) - ln(c) \\ ln(b^c) = c * ln(b) \\ \\ e^a * e^b = e^{a+b} \\ (e^a)^b = e^{a+b} \\ e^{-a} = \frac{1}{e^a} \\ ln(e^a) = a \)

weitere Rechenregeln#

Abrundungsfunktion / Gaußklammer [ ]: \([3.34] = 3\)

Fakultät: produkt aller natürlichen Zahlen bis n ist n!

  • BSP: \(4! = \prod_{i=1}^4 i = 1 * 2 *3 * 4 = 24\)

  • 1! = 1 und 0! = 1

Binomialkoeffizient: \(\binom{n}{k} = \frac{n!}{k!(n - k)!}\)