02.06.2022 Schätzer

Punktschätzer

direkte Angabe eines Punkts für Parameter von Interesse

• Merkmal X

• Verteilung von X charakterisiert durch Parameter

• \(X_1,...,X_n\) unabhänhig und identisch wie X verteilt

Punktschätzer:

• Funktion \(t(X_1,...,X_n)\)

• Anwendung der Funktion auf Beobachtungswerte \(t(x_1,...,x_n)\)

Gütekriterien

Erwartungstreue:

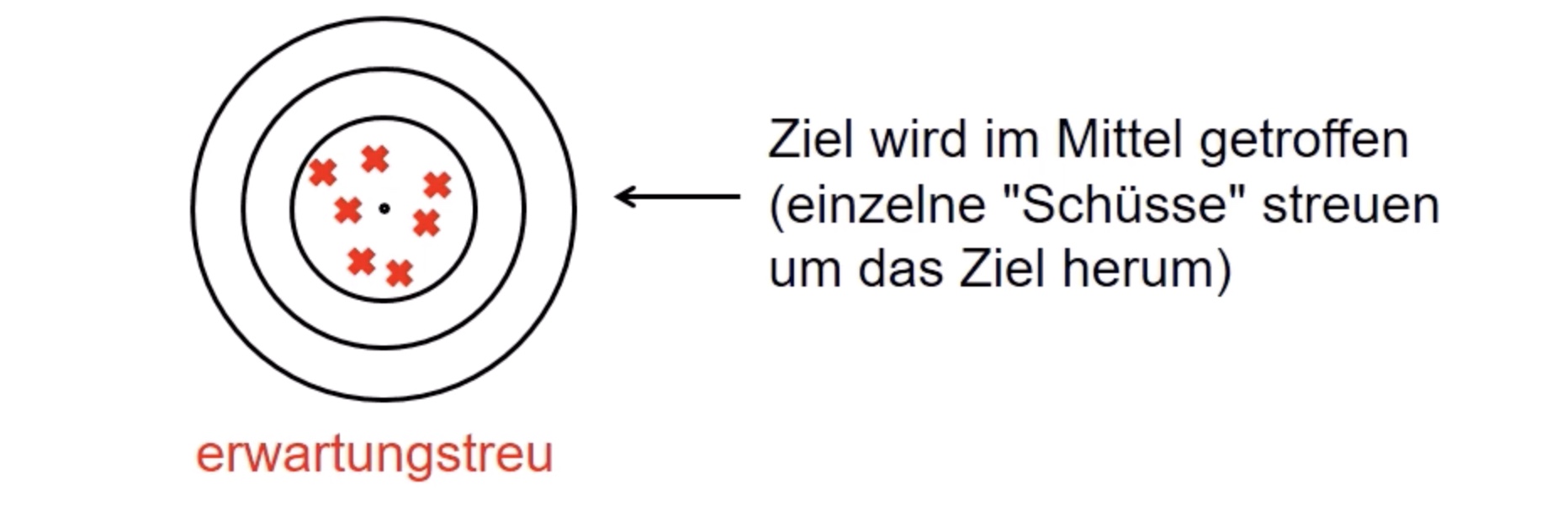
außerdem geringe Varianz um den Mittelpunkt

Formal:

• \(t(X_1,...,X_n)\) als Schätzer für Parameter \(\theta\)

• Erwartungstreu, wenn \(E(t(X_1,\dots,X_n)) = \theta\)

Varianzschätzer

verschiedene Schätzer: $\( 1)\ \tilde{S}^2 = \frac{1}{n} \sum (X_i-X_n) \text{ mit } E(\bar{S}^2) = \frac{n-1}{n} \sigma^2 \\ 2) \ S^2 = \frac{1}{n-1} \sum (X_i-X_n) \text{ mit } E(S^2) = \sigma^2 \)$

Intervallschätzer

Interesse ist Angabe eines Intervalls, das den Parameter enthält

• X Zufallsvariable

• Verteilung von X = \(\theta\)

Wahrscheinlichkeit \(\alpha\) (\(0 \le \alpha \le 1\)) gegeben (auch Irrtumswahrscheinlichkeit)

Definition

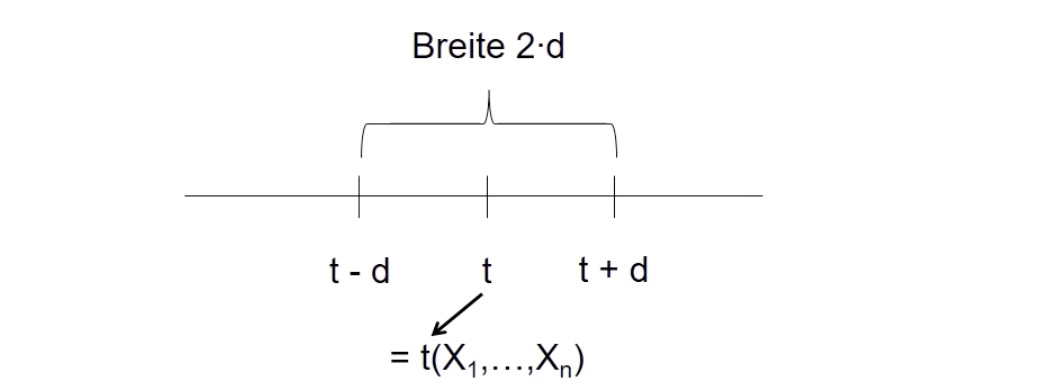
Konfidenzintervall: \([K_u,K_o]\) Mit

• Untergrenze \(K_u = K_u(X_1,...,X_n)\)

• Obergrenze \(K_o = K_o(X_1,...,X_n)\)

Sodass \(P ( \theta \in [K_,K_o]) = \underbrace{1-\alpha}_{\text{Konfidenzniveau}}\)

Eigenschaften

Oft: symmetrische Konfidenzintervalle, insb. bei symm. Schätzern

Konfidenzintervall bei Normalverteilung

symmetrisches Konfidenzintervall für \(\mu\);

=> Suche: Konfidenzintervall der Art: \([\bar{X}-d, \bar{X}+d]\)

---

\(\sigma^2\) bekannt: $\( \Big[\bar{X}- \frac{\sigma}{\sqrt{n}}\cdot z_{1-\alpha/2} \ , \ \bar{X} + \frac{\sigma}{\sqrt{n}}\cdot z_{1-\alpha/2}\ \Big] \)\( für \)(1-\alpha)$ Konfidenzintervall

---

\(\sigma^2\) Unbekannt:

• als Schätzer für Sigma S = Varianz der Beobachtungen

• \((1-\alpha/2)\) Quantil der t-Verteilung statt z

\[ \Big[\bar{X}- \frac{S}{\sqrt{n}}\cdot t_{(n-1;1-\alpha/2)} \ , \ \bar{X}+ \frac{S}{\sqrt{n}}\cdot t_{(n-1;1-\alpha/2)}\Big] \]

für \((1-\alpha)\) Konfidenzintervall

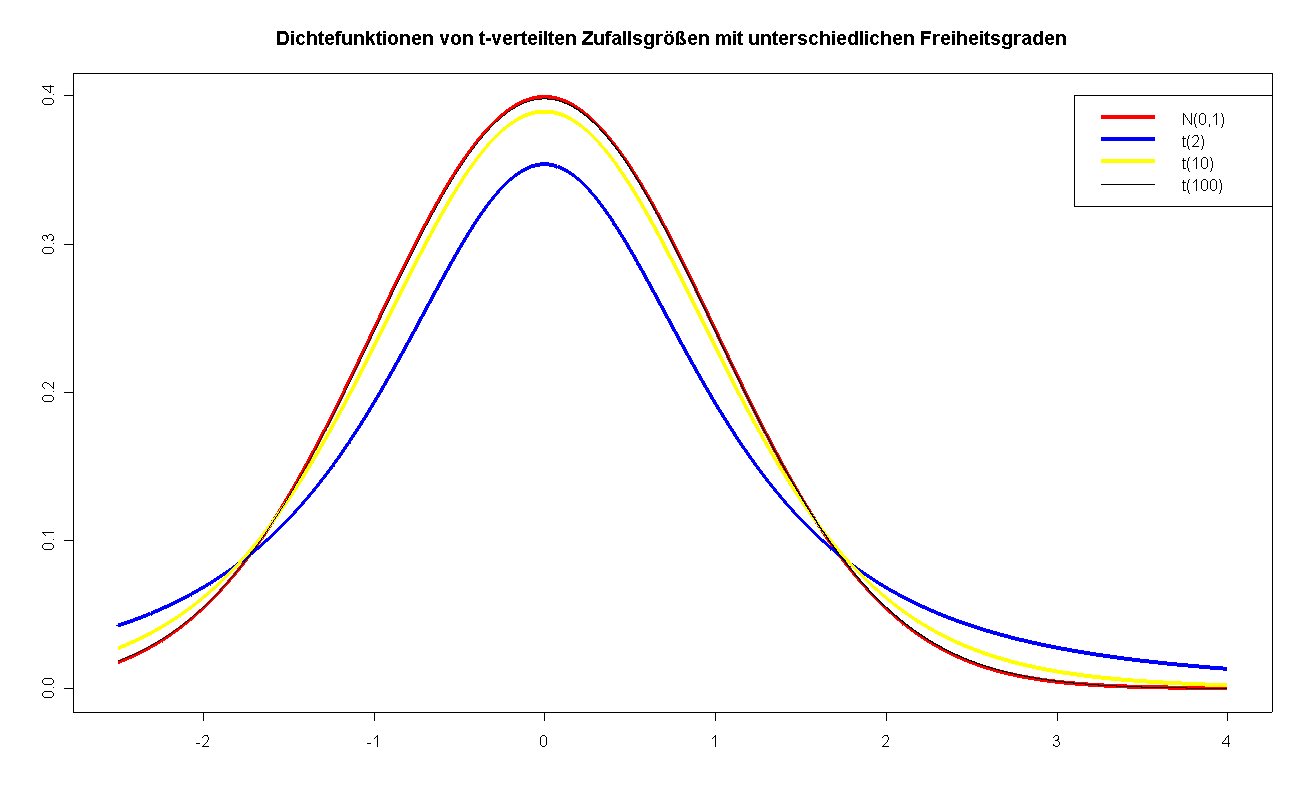
Exkurs: t-Verteilung:

• DIche symmetrisch um 0

• Glockenform ähnlich zu Normalverteilung

• stellt SNV ab n=30 dar (\(t_N \to N(0,1)\))

Beispiel Lohnverteilung

• unterstellt Normalverteilung für Lohn X

• \(\sigma^2\) unbekannt

aus Stichprobe:

• n = 39

• \(\bar{x} = 7.77\)

• s = 0.46

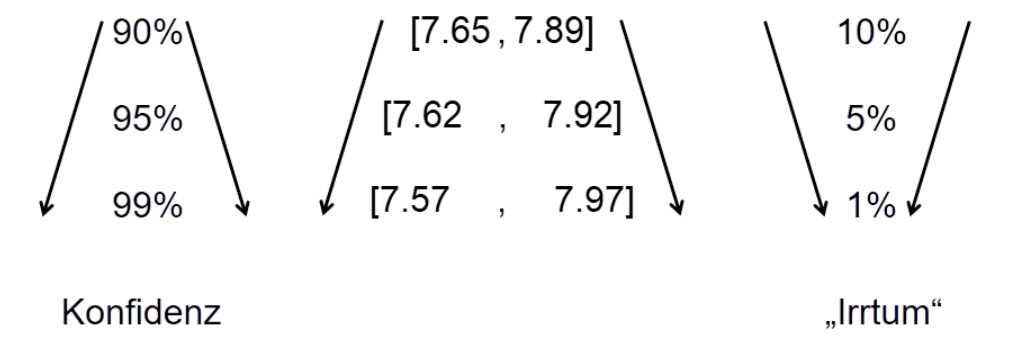
wähle \(\alpha = 0.1,0.05,0.01\)

Ergebnis: