22.11.2022 Verteilungen von Einkommen

Einkommenspyramiden

Einkommenspyramiden: nach Niehues

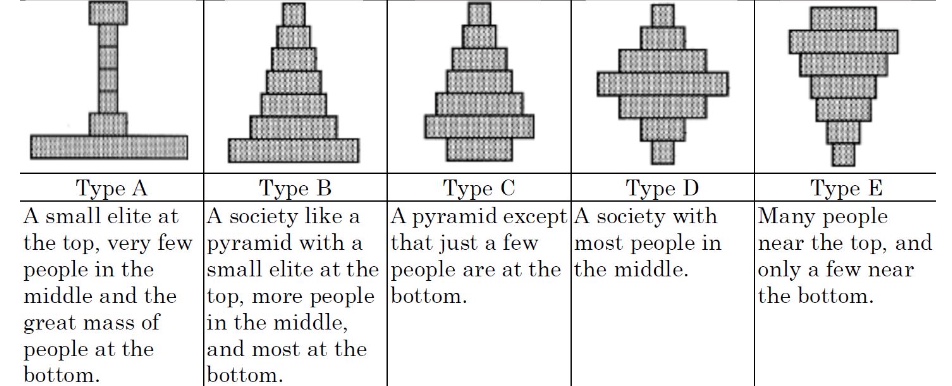
Deutschland: Ansicht vs Realität

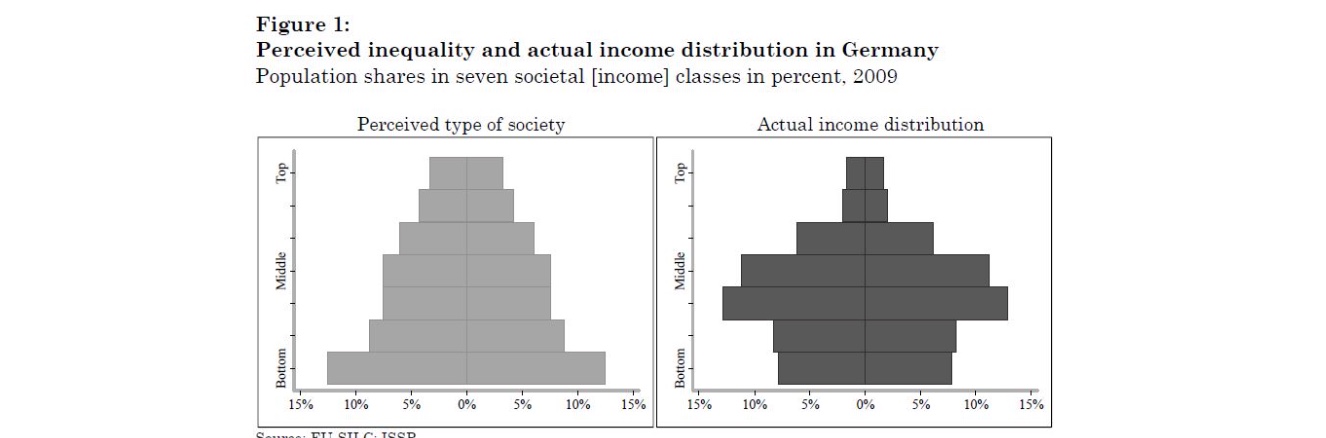
Parametrische Verteilungen

weil Einkommen zu unsymmetrisch: parametrische, kontinuierliche Verteilungen, bspw. Lognormal

• stetig differenzierbar

• Ableitung der Funktion = Dichtefunktion: \(F'(x) = f(x)\)

• gesamte Verteilung darstellbar

Lognormalverteilung

Parameter:

• \(\mu\) = Lage

• \(\sigma\) = Skalierung (höher = ungleicher)

\[ F(x) = \Phi \Bigg(\frac{ln(x)-\mu}{\sigma}\Bigg) \]

\(\Phi\) = Standardnormalverteilung (SNV)

• Definitionsbereich \(x > 0\)

• Mittelwert: \(\bar{u} = e^{u+\frac{1}{2}\sigma^2}\)

• Median: \(m = e^\mu\)

• Modus = \(e^{\mu-\sigma^2}\)

Modus < Median < Mittelwert !

Verteilungsfunktion	Dichtefunktion

• empirisch gut darstellbar

• teilweise Mängel an Enden

Beispiel: UK-Wochenlohn Vollzeit, Männer

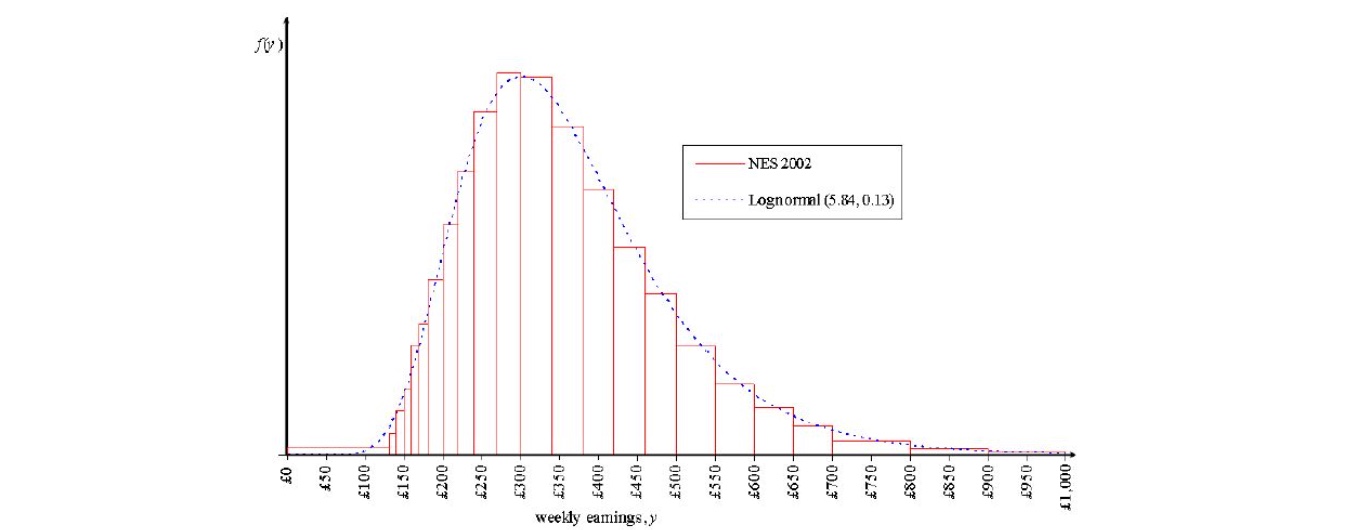
Paretoverteilung

für reiche Bürger in einem Land / ungleiche Länder

\[ F(x) = 1- \bigg( \frac{x_{min}}{x}\bigg)^{\alpha} \]

• immer fallend

• \(\alpha > 0\) = Parameter für die Form (höher = gleicher)

• \(x_{min}\) = Einkommensuntergrenze

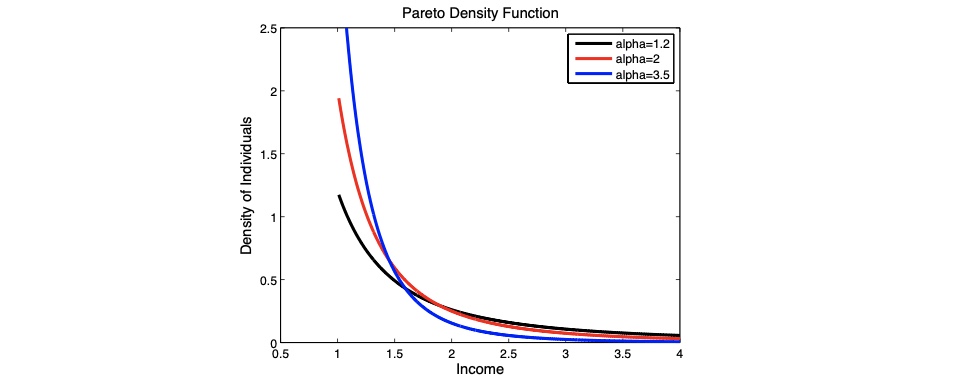
Warum höheres Alpha = besser? weil weniger extrem Reiche = kleinere Ungleichheit

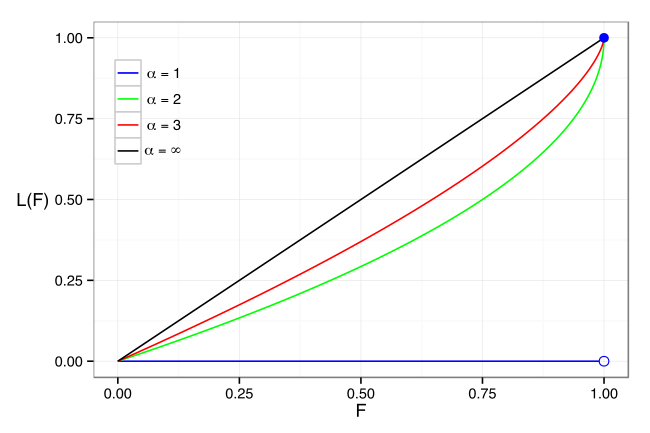
Ungleichheitsmaße

für Vergleiche über Länder hinweg

Eigenschaften Ungleichheitsmaße

• Unabhängigkeit Mittelwert

• unabhängig Bevölkerungsgröße

• Symmetrie

• Pigou Prinzip: Transfer senkt Ungleichheit

• wünschenswert: Zerlegbarkeit

Variationskoeffizient CV

Verhältnis Standardabweichung Einkommen und Durchschnittseinkommen $\( CV = \frac{\sqrt{Var}}{\bar{u}} \)$ je höher, desto ungleicher

wenn Lognormalverteilung: $\( CV = \sqrt{(e^{{\sigma}^2}-1)} \)$ Nachteile:

• Schiefe außer Acht

• Oberer Bereich sensitiver als unten

Gini

Fläche zwischen Lorenzkurve und Gleichverteilung durch Gesamt

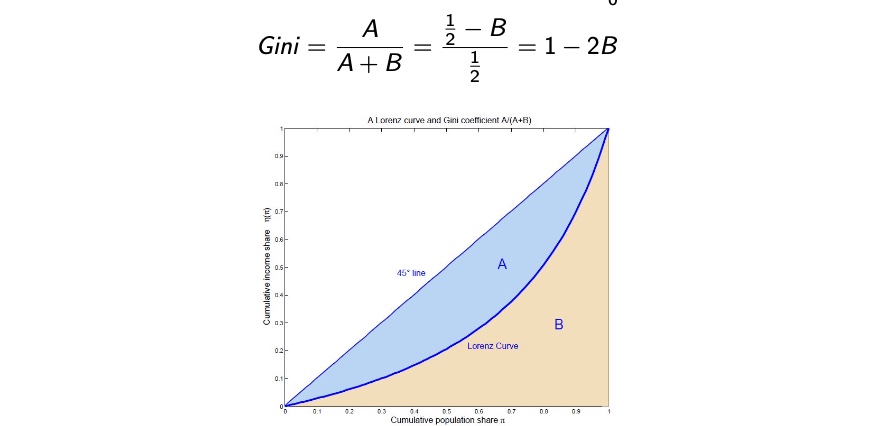
• zwischen 0 und 1

• Sensitiv in Mitte

Berechnung	Formel
Lognormal	\(2 \Phi (\frac{\sigma}{\sqrt{2}})-1\)
Pareto	\(\frac{1}{2 \alpha-1}\)
Individueen (alternativ)	$\frac{E

Alternative = erwartete Differenz zwischen zwei Individuuen

Berechnungstabelle

Einkommen y	Anzahl Individueen x	rel. Anteil x	kum. x	Rel. Anteil y	kum . Anteil y

Theil Index

\[ Theil = \frac{1}{N} \cdot \sum_{i=1}^N \frac{y_i}{\mu} \cdot ln(\frac{y_i}{\bar{u}}) \]

• zwischen 0 und \(ln(N)\)

• sensitiv in MItte und Verteilung

auch aufteilbar zwischen Gruppen

Empirie

Gini auf der Welt

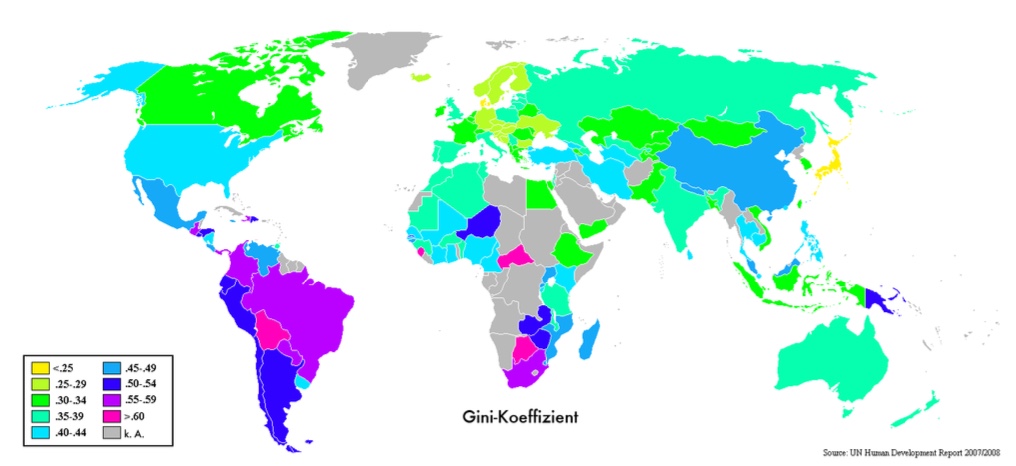
Verglech zw. Koeffiiznenten

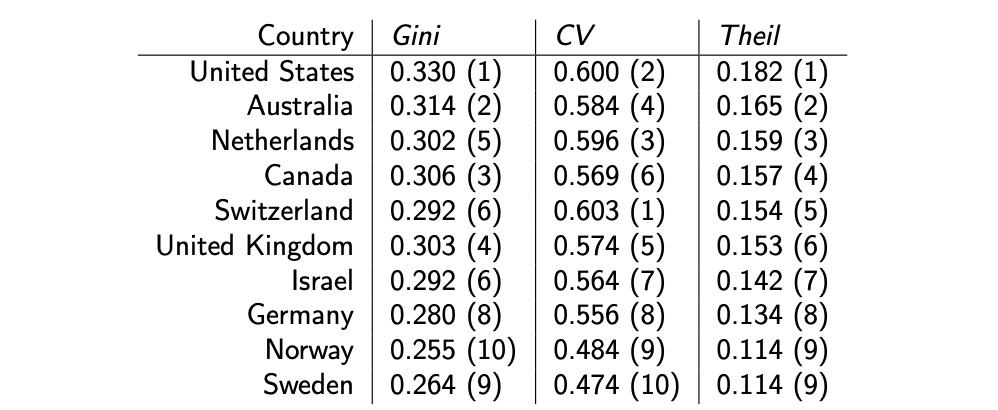
=> CV ist stark unterschiedlich, weil obersensitiv

Faktoren der Ungleichheit:

• Sektore Struktur der Wirtschaft

• Steuer / Transfersystem

• staatliche Ineffizienzen

• Toleranzgrenzen Ungleichheit