27.04.2023 Banks#
Chapter 10: Banks, Money and Credit Market
Money = medium of exchange for trade (requires trust)
Intertemporal Optimization#
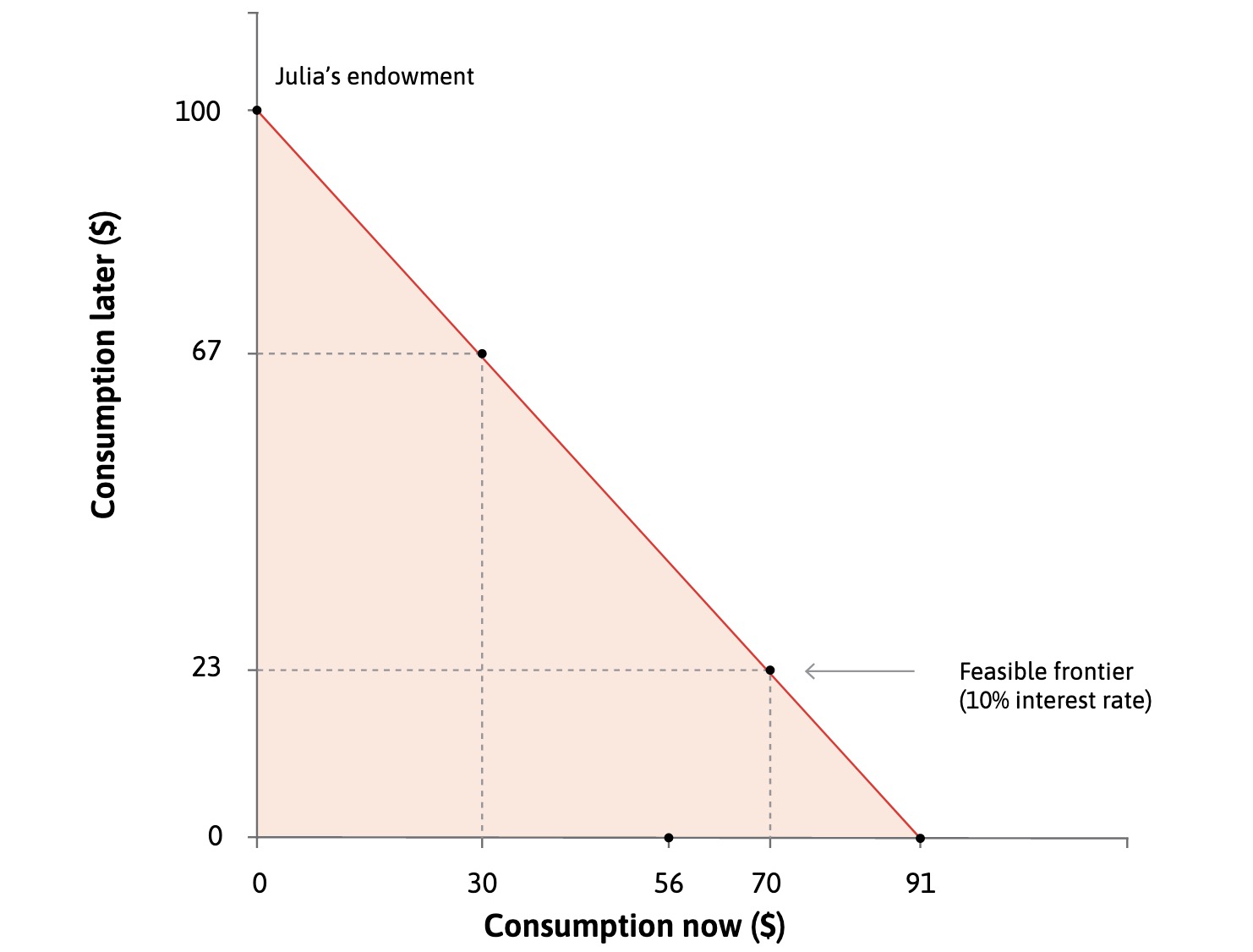
Borrowing brings consumtpion to Future
r = interest rate
tradeoff = 1+r
Repayment = principal + interest rate
\(91 (1+r) = 100\) , with r=10%
Decisions#
based on preferences of the consumer
individuals want to smooth consumption
overly high consumption in one period = costly
Impatience: Preference for present consumption
measured by discount rate
affected by desire to smooth consumption
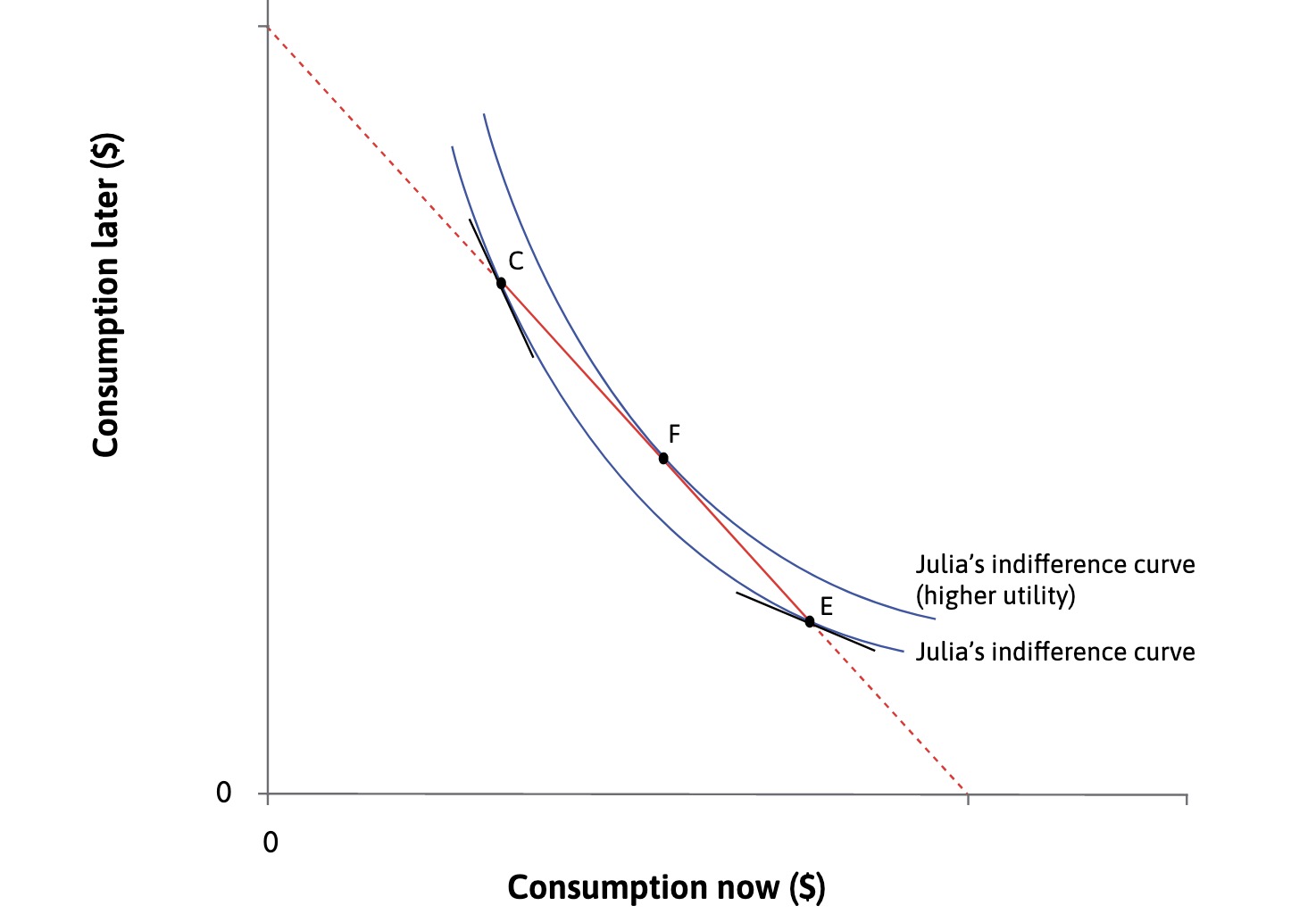
Equilibrium#
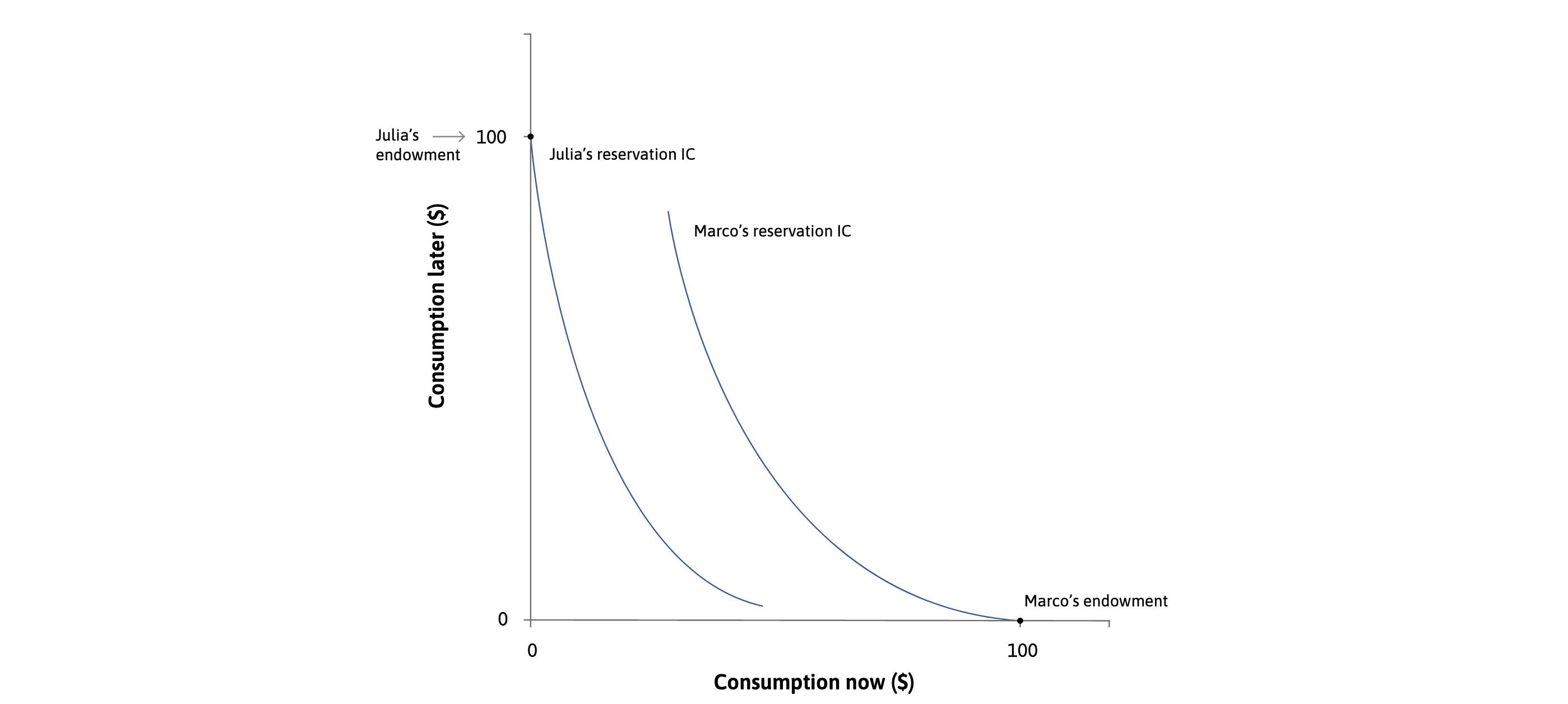
at Point where $\( MRS = MRT \implies 1+p = 1+r \)$ with different endowments
Julia = 100 in future (wants to borrow)
Marco = 100 now (wants to save)
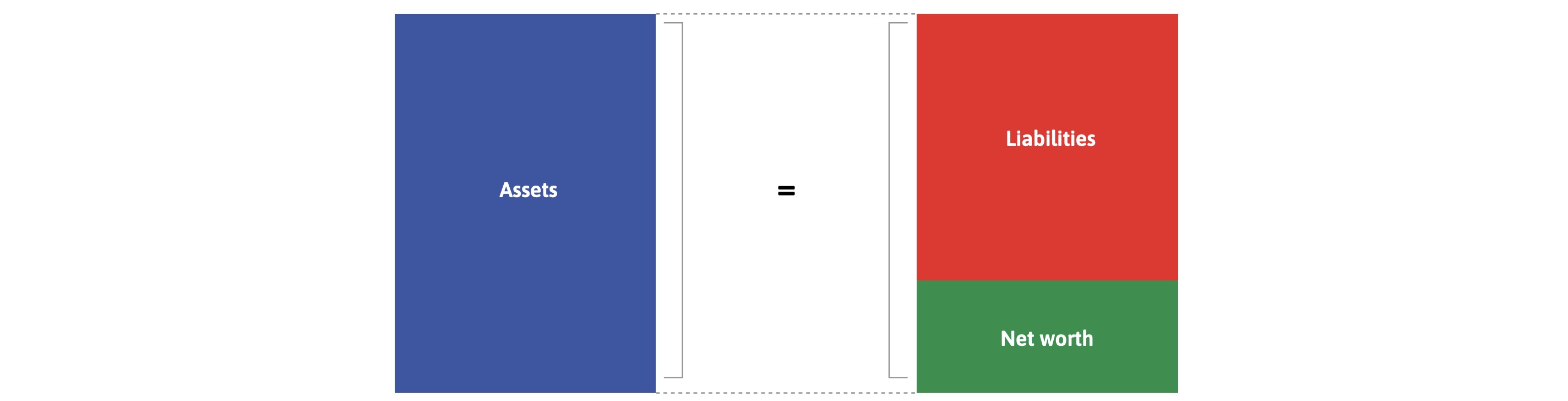
Balance#
Assets = what person owns
Liabilities = what person owes
Net Worth = Assets - Liabilites
not impacted by borrowing etc.!
Banking System#
Definition
Bank: a firm that makes profits by lending and borrowing
Central Bank: bank owned by government with money creation monopoly
Structure of the System
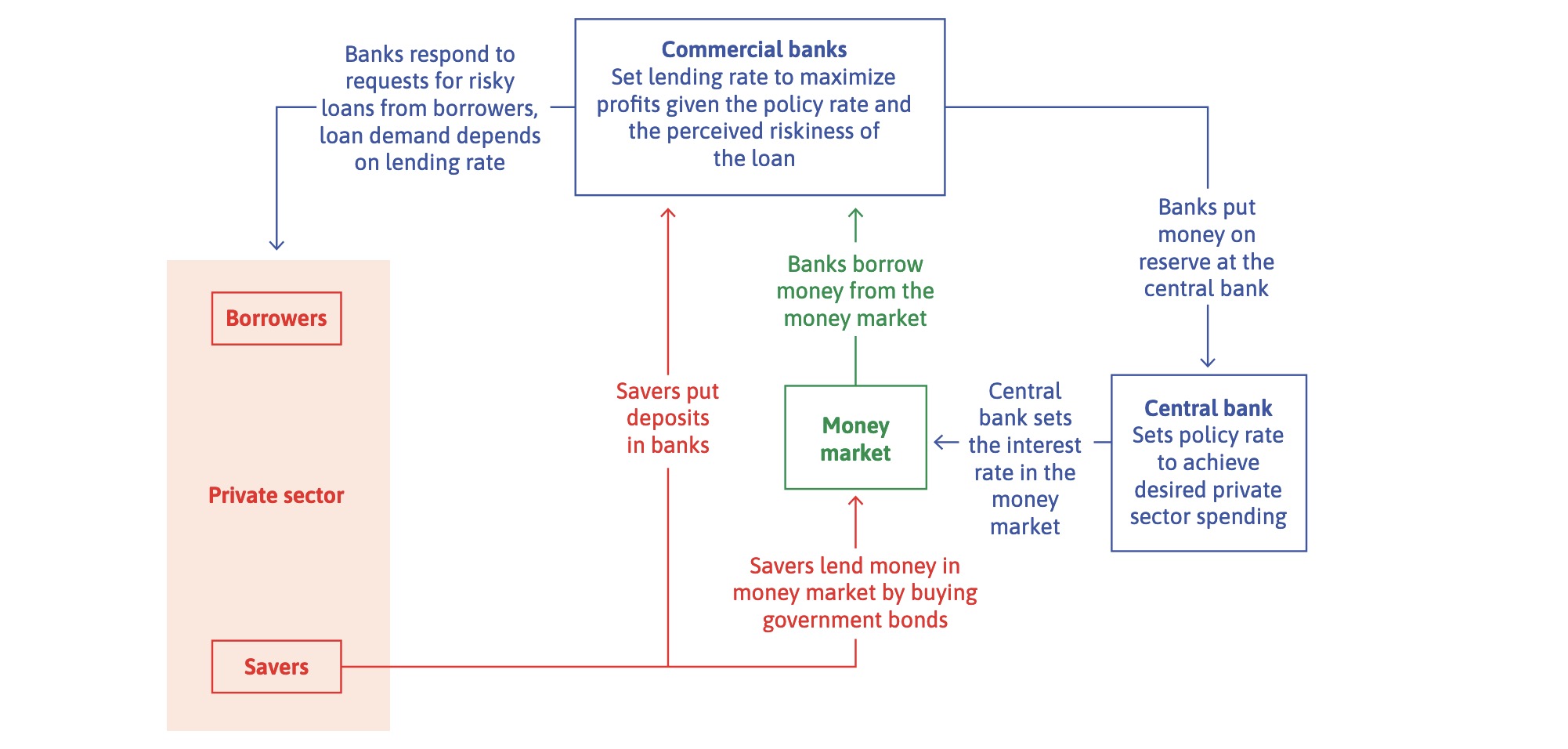
policy interest rate = set by CB
bank lending rate = banks rate on consumer loans
banks set lending rate \(r > r^p\) policy rate and based on:
Risk of default
risk tolerance
amount of bank equity
degree of competition in banking sector
the higher \(r \uparrow \implies L^S \downarrow\) Liquidity Supply lower
Setting the Rate / Liquidity#
based on the interest rate
Formula for Rate $\( r = (1+ \mu^B) \ r^P ,\text{ with mark-up} = \mu^B \)$
Profit of a commercial Bank: $\( V_B = \frac{rL^S - r^p (L^S-D-e)}{e} -\frac{var(v)}{2 \tau}* \frac{L^S}{e}^2 \)$
r = lending rate
\(r^p\) = policy rate
\(L^S\) = credit supply
\(D\) = customer deposits
\(e\) = equity
\(\tau\) = risk tolerance
\(v\) = uncertain part of returns on loands
\(var(v)\) = riskiness of v
Terms explained:
\(rL^S\) = interest return on Loans
\(rL^S - r^p (L^S-D-e)\) = financing costs for credit not backed
\((\frac{L^S}{e})^2\) = Bank Leverage
\(var(v) * \frac{L^S}{e}^2\) = total risk of bank
Refinancing Options of Banks:
Interbanking Market
loans from CB
new deposits
Derivation
What is the optimal credit supply? $\( \frac{\delta V_B}{\delta L^S} = \frac{r-r^p}{e} -\frac{var(v)L^S}{\tau e^2} = 0 \)\( rewrite to determine the mark-up \)\( r - r^p = \frac{var(v)L^S}{\tau e} \\ \implies L^S = \frac{\tau e}{var (v)} * (r-r^p) \)$ logic: when to supply more?
higher risk tolerance \(\tau\)
higher equity \(e\)
larger proft margin (markup) = higher incentive to supply
higher risk = lower supply
Demand Liquidity#
credit demand of private sector $\( I = L^D = \bar{I} - a * r \)\( Equilibrium: \)\( \overbrace{\frac{\tau e}{var (v)} * (r-r^p)}^{Supply} = \overbrace{\bar{I}-a*r}^{Demand} \)\( solve for r \)\( r [\frac{\tau e}{var (v)}+a] = \frac{r^p \tau e}{var(v)}+ \bar{I} \\ \)\( leads to: \)\( r = \frac {\frac{r^p \tau e}{var(v)}+ \bar{I}} {\frac{\tau e}{var (v)}+a} = \frac{r^p + \frac{\bar{I}* var(v)}{\tau e}} {1+ \frac{a * var(v)}{\tau e}} \)$ Conclusions: interest rate increases:
with higher autonomous demand I : more competition for loans
with higher policy rate \(r^p\)
=> in exam: do math and get points