18.10.2022 Solow Modell#
Kaldors Fakten#
„Stylized Facts“, die ein Modell erfüllen muss
p.P Einkommen = konstante Wachstumsrate
Verhältnis Kapital-Output konstant
Kapital / Arbeit Anteil am Output relativ konstant
Rendite r ist relativ konstant
Solow#
Produktionsfunktion#
Produktionsfunktion: \(Y = F(K,L)\)
Annahmen:
Produktionsfunktion stetig, zweimal differenzierbar, konkav
konstante Skalenerträge, abnehmende Grenzerträge
L = Anzahl Arbeiter
Unternehmen#
viele Unternehmen
homogenes Output
perfekter Wettbewerb
Preisnehmer K,L
Gewinn: \(\Pi =K^a L^{1-a} - (rK+wL)\)
\(a \frac{Y}{K}= r = MP_K\)
\((1-a) \frac{Y}{L} = w = MP_L\)
Output: \(Y = wL+rK\)(Gewinn ist null)
Anteil Kapital an Output = a
Anteil Arbeit an Output = 1-a
Emprisch: \(a=1/3\)
Pro-Kopf-Output#
per Capita Output: \(y = \frac{Y}{L}\)
\(\to y = k^a =f(k)\)
Wachstumsrate: $\( \frac{\delta \ln(y)}{\delta t} = a (\frac{\delta \ln(K)}{\delta t}-\frac{\delta \ln(L)}{\delta t}) \)$
Kapitalakkumulation#
Annahme: L ist konstant, Ersparnisse = Investitionen
Veränderung des Kapitals = Investitionen - Abschreibung $\( \dot{K} = I-D =sY -\delta K \)$
s = Sparquote
\(\delta\) = Abschreibungsquote
Wachstum Pro-Kopf-Kapital \(\frac{\dot{k}}{k}=s\frac{y}{k}-\delta\)
Solow Diagramm: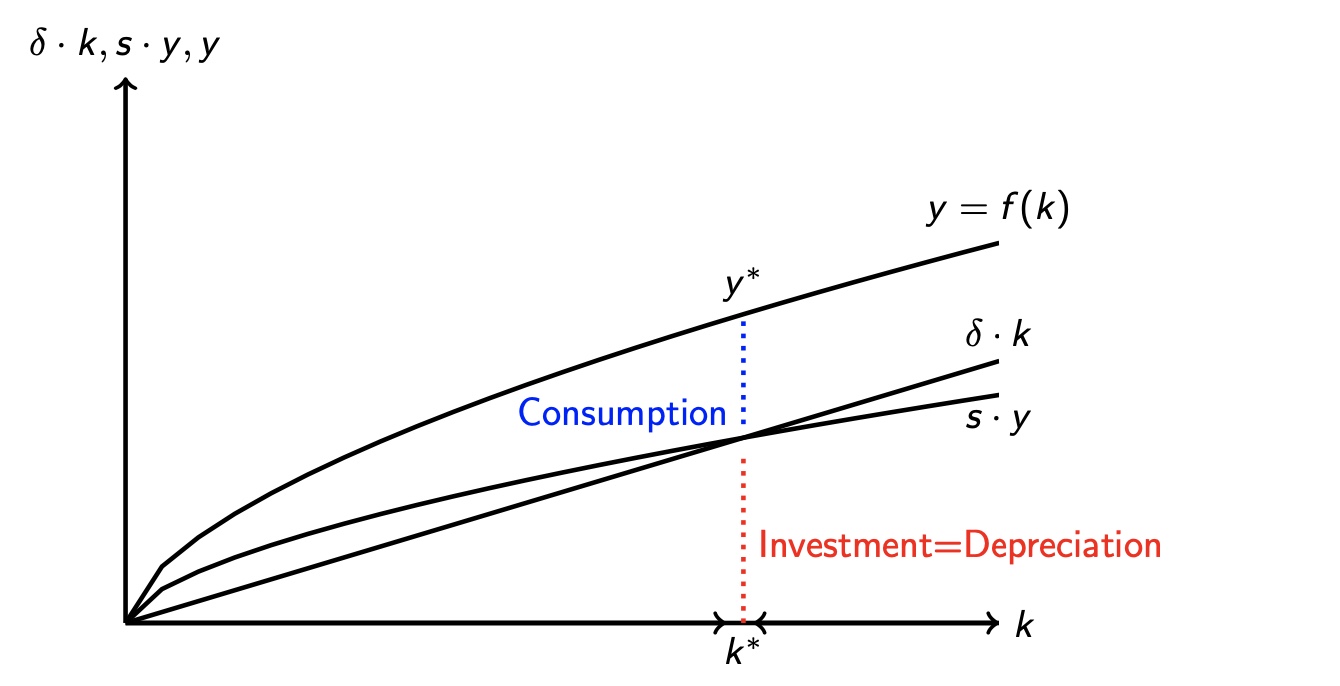
Kapital wächst bis zum Steady State, dort Investment = Abschreibungen
-> Wachstumsrate = 0
Lösung des Modells#
zu erklärende Variablen: Y und K
exogene Variablen: \(a,s,\delta, k_0, n\) (Bevölkerungswachstum) $\( k^* = \Big(\frac{s}{\delta}\Big)^{\frac{1}{1-a}} \\ y^* = (k^*)^a = \Big(\frac{s}{\delta}\Big)^{\frac{a}{1-a}} \)$ je höher die Sparquote -> höheres Pro-Kopf-Einkommen
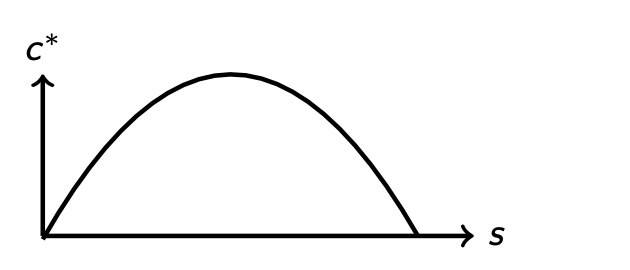
Tradeoff bei Sparquote:
mehr s = höherer Steady State = höheres Einkommen = höherer Konsum
höhere Sparquote = niedrigerer Konsum
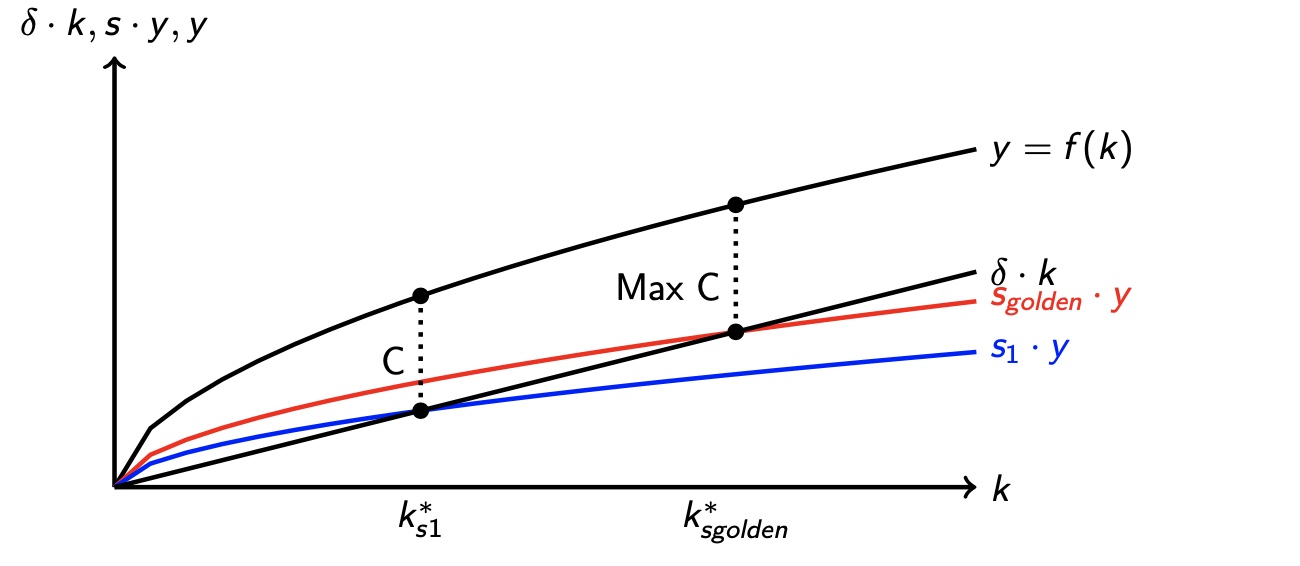
Goldene Regel der Sparquote#
das Maxmimum an Konsum ist an \(s^*\) erreicht $\( f' (k^*(s)) = \delta \)$ führt zu: Grenzprodukt des Kapitals = Abschreibungen des Kapitals
Grenzprodukt des Kapitals = Steigung der Produktionsfunktion
Beispiel:
\(\delta = 0.05\)
\(a = 0.5\)
\(s = 0.2\)
Rechnugn zu Steady State, Einkommen und Konsum $\( k^* = \Big(\frac{s}{\delta}\Big)^{\frac{1}{1-a}} = \Big(\frac{0.2}{0.05}\Big)^{\frac{1}{1-0.5}} = 16 \\ y^* = (k^*)^a = (16)^{0.2} = 4 \\ c^* = y^* - s \cdot y^* = 4-0.2 \cdot 4 = 3.2 \)\( Optimale Sparquote wäre: (**nur im Cobb-Douglas!**) \)\( f' (k^*(s)) = \delta \\ \to s^* = a = 0.5 \)$
Fazit zu Solow#
Empirie zwischen Sparquote und Einkommen
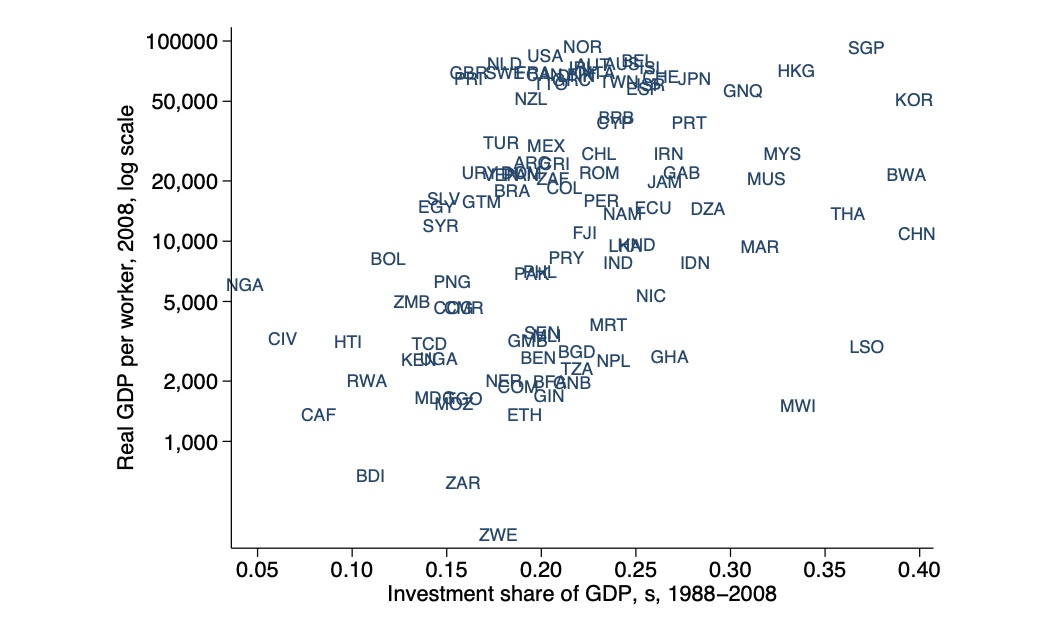
= genereller Korrelation, aber wesentlich mehr Erklärungsfaktoren
Wachstum nur durch Kapitalakkumulation
unzureichend für Einkommensunterschiede zwischen Ländern