02.11.2022 Marshall Nutzenfunktion#
Entscheidungsproblem eines Komnsumenten
Budget I (Income)
Preise von Gütern x,y
Budgetbedingung \(I = p_x x + p_y y\)
Budget wird vollständig ausgegeben
Präferenz Trade off (innerer Tradeoff des Konsumenten)
Grenzrate der Substitution
Markt Trade-off (Verhältnis der Preise)
Grenzrate der Transformation
im Optimalpunkt
Steigung der Budgetgerade = Steigung der Indifferenzkurve
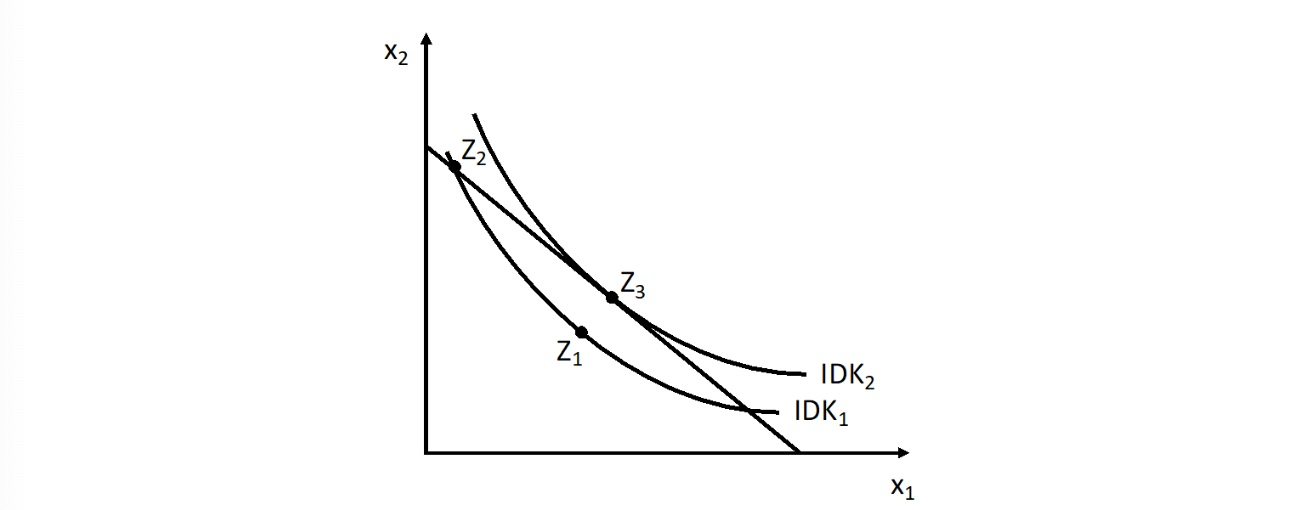
Lagrange Ansatz#
Optimierungsproblem: $\( \max U(x,y) \ s.t \ p_x x+ p_yy \le I \\ \to L = U(x,y)+ \lambda (I-p_x x-p_y y) \)\( Jetzt: Ableiten (\)x,y,\lambda\() und 0 setzen \)\( I.\frac{\partial L}{\partial x} = \frac{\partial U}{\partial x} = MU_x - \lambda p_x = 0\\ II.\frac{\partial L}{\partial x} = \frac{\partial U}{\partial y} = MU_y - \lambda p_y = 0\\ III.\frac{\partial L}{\partial \lambda} = I-p_x x-p_y y = 0 \)$
aus 1. und 2: $\( \lambda = \frac{MU_x}{p_x} = \frac{MU_y}{p_y} \\ \frac{MU_x}{MU_y} = \frac{p_x}{p_y} \to MRS = MRT \)$
\(\lambda\) = Schattenpreis
Nutzenveränderung einer kleinen Einkommensänderung
also leichte Lockerung der Budgetrestriktion
nur ordinal interpretierbar!
Marshallsche Nachfrage#
Marshallshe Nachfragefunktion: von Gut nachgefrage Menge abhängig von Preisen und Einkommen
Notation: \(d_x (p_x, p_y, I)\)
Erklärung von Nachfrageänderung bei Preisänderung etc
Math. : Menge von Tangentialpunkten zwischen Indifferenzkurven
Veranschaulichung:
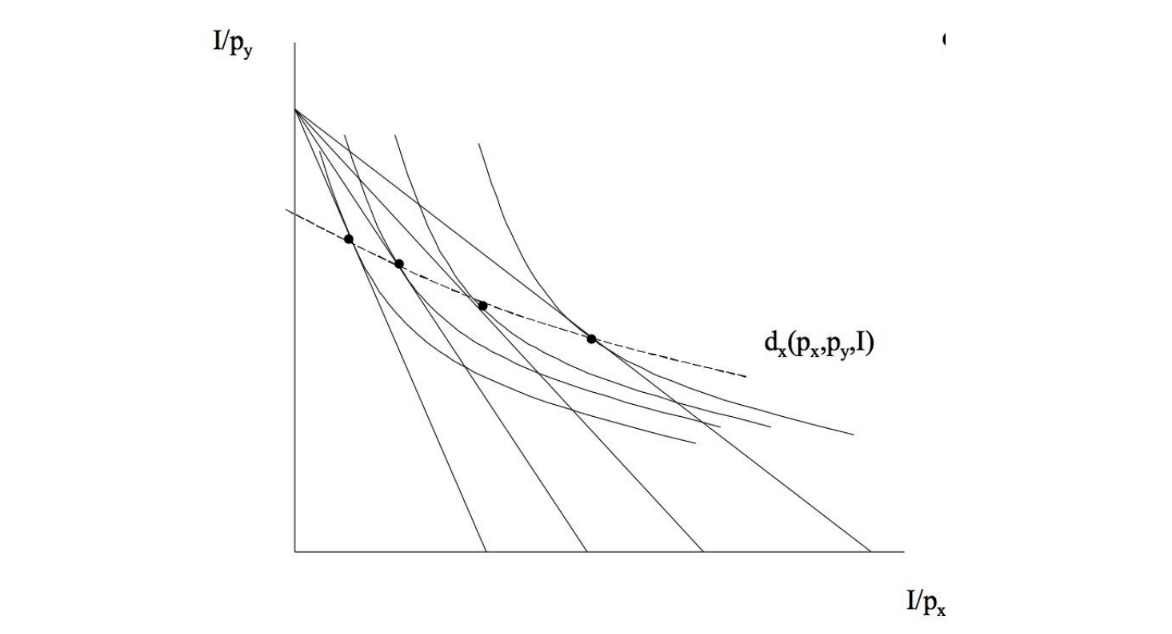
Übung dazu#
Marshallsche Funktion $\( \max U(x,y) \ s.t \ p_x x+ p_yy \le I \\ \to L = A \cdot x_1^a \cdot x_2^b+ \lambda (I-p_1 x-p_1 y) \)\( Ableitungen \)\( \begin{aligned} I.\frac{\partial L}{\partial x} &= A \cdot a x_1^{a-1} \cdot x_2^b - \lambda p_1 = 0\\ II.\frac{\partial L}{\partial x} &= A \cdot b x_2^{b-1} \cdot x_1^a - \lambda p_2 = 0\\ III.\frac{\partial L}{\partial \lambda} &= I-p_1 x-p_2 y = 0 \end{aligned} \)\( Folgerungen (I und II nach Lambda umstellen) \)\( \lambda = \frac{A \cdot a x_1^{a-1} \cdot x_2^b}{p_1} \\ \lambda = \frac{A \cdot b x_2^{b-1} \cdot x_1^a}{p_2} \\ \to x_2(x_1) = \frac{b}{a} \cdot \frac{p_1}{p_2} \cdot x_1 \)\( in III einsetzen und voilà \)\( x_1^* (p_1,p_2, I) = \frac{I}{p_1} \cdot \frac{1}{1+ \frac{b}{a}} \\ x_2^* (p_1, p_2, I) = \frac{I}{p_2} \cdot \frac{b}{a+b} \\ \)$ das sind die Optima
Schlussfolgerungen (bei Gut 1)
steigt \(p_1\), sinkt Menge von \(x_1\)
wenn \(I\) steigt, steigt auch \(x_1\)
\(p_2\) hat keinen Einfluss auf Menge für \(x_1\)
nicht immer!
Indirekte Nutzenfunktion#
gibt maximalen Nutzen bei geg. Einkommen und Preisniveau an
aus direkter Nutzenfunktion
praktisch, weil man nicht andauernd Optimierungsproblem neu berechnen muss
mit p = Preisvektor
Notation: \(V(p, I) = U(x^* (I,p) , \ x*(I,p))\)