18.01.2022 Regression + Zeitreihen#
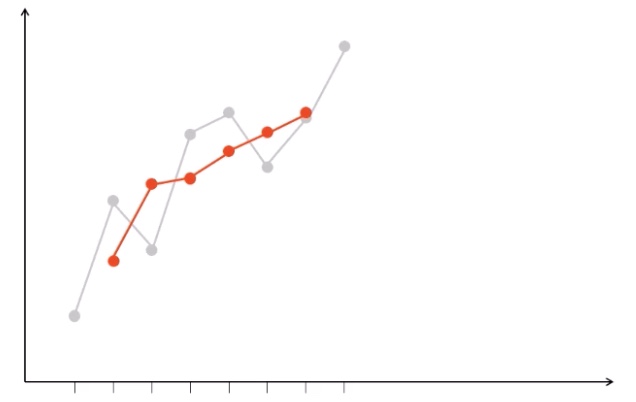
Einfaches lineares Regressionsmodell#
Regressionsmodell: statistische Analyse für Untersuchung von Wirkungszusammenhängen
für angenommenen linearen Zusammenhang zwischen x, y
$\(
Notation: y = a * x + b + \epsilon
\)$
y : Zielgröße
x : Einflussgröße
\(\epsilon\) : zufällige Störgröße
a,b : Regressionskoeffizenten (Parameter der Regressionsfunktion)
Bestimmen der Koeffizenten mit verschiedenen Methoden
Kleinste-Quadrate-Methode \(\bold{R^2}\)#
teste verschiedene Geraden und minimiere die Abstände zur Gerade
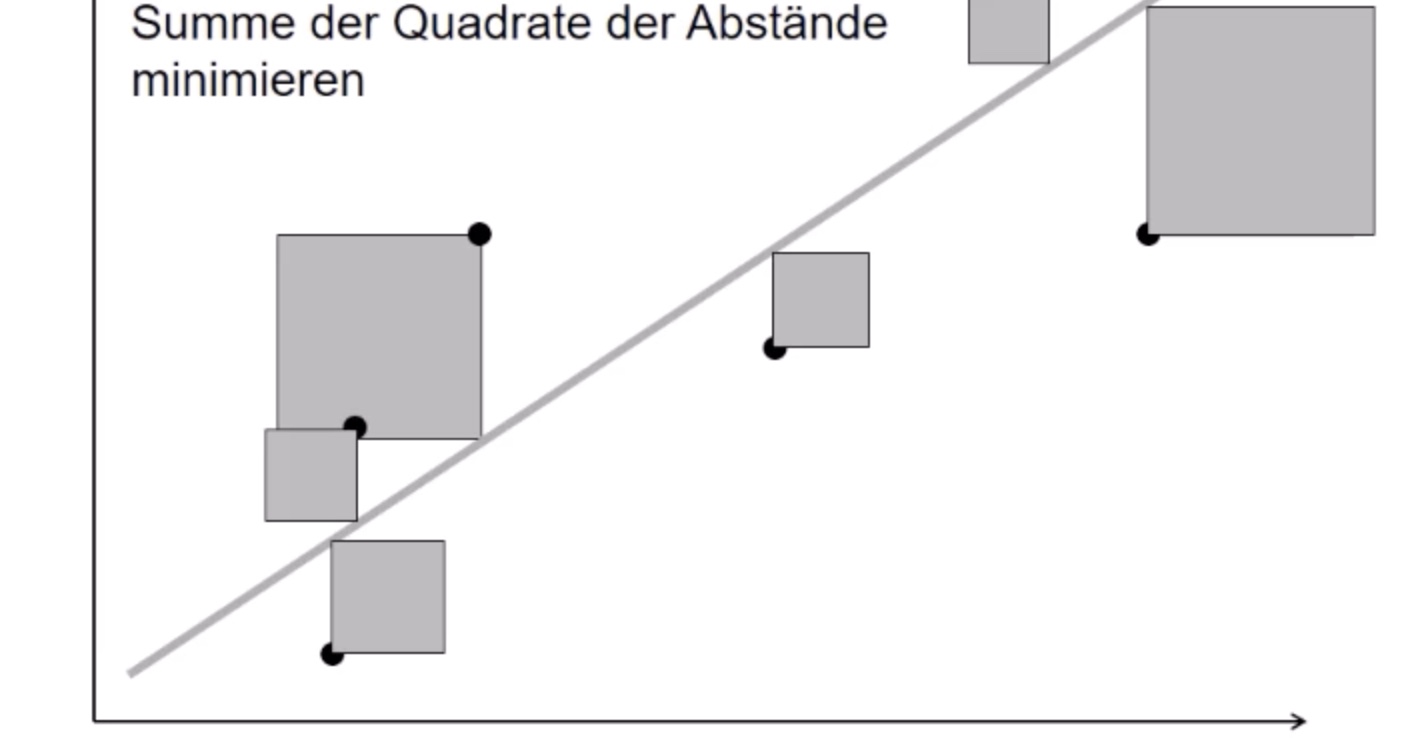
Formeln: $\( \hat{a} = \frac{ \sum x_i * y_1 - n * \bar{x} * \bar{y} }{ \sum x_i^2 - n * \bar{x}^2 } \\ \hat{b} = \bar{y} - \hat{a}*\bar{x} \)$
Prognosen: \(\hat{y} = \hat{a} *x+\hat{b}\)
Residuen: \(\hat{\epsilon}_i = y_i - \hat{y}_i\)
Werte mit ^ bezeichnen berechnete Ergebnisse
Beurteilung der Modellqualität#
Bestimmtheitsmaß \(R^2 = \frac{(s_{\bar{Y} })^2 }{(s_Y)^2 }\)
Varianz der berechneten durch Varianz der beobachteten Werte
also R^2 = Anteil erklärter Streuung an Gesamtstreuung
Wertebereich 0 < R < 1
Analyse zeitlicher Verläufe#
zwei Methoden:
Zeitreihenanalyse : Verlauf der zeitlichen Entwicklung
Indexrechnung : Vergleich zweier Zeitpunkte
Zeitreihen#
Merkmal Y beobachtet \(y_1,...,y_t\) zu Zeitpunkten t = 1,…,T
Beispielhafte Muster:
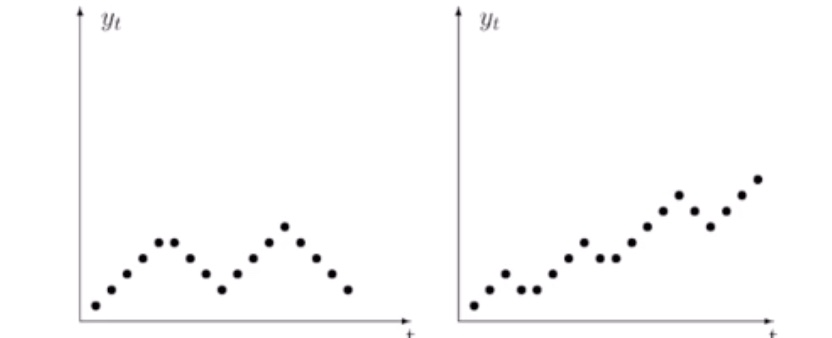
zyklische Schwankung (links) und zyklisch + Aufwärtstrend (rechts)
Zeitreihe = meist aus mehreren Komponenten:
Trend -> langfristig, g
Saison -> kurzfristig, s
Zufall, irregulär, \(\epsilon\)
Ziel: Trennung der Komponenten
Arten der Komponentenmodelle
additives Modell: \(y_t = g_t + s_t + \epsilon_t\)
multiplikatives Modell: \(y_t = g_t * s_t * \epsilon_t\)
logarithmiert: \(log(y_t) = log(g_t) + log(s_t) + log(\epsilon_t) \)
Lineares Trendmodell#
analog zur Regression mit Zeit: \( y_t = a * t + b + \epsilon_t \)
resultiert in Trendgerade
Glättung mit Moving-Average#
gleitender Durschschnitt zur Glättung von Werten
berechne für jeweils 3 Werte Durchschnitt
platziere Durchschnitt in Mitte der 3 Werte
wiederhole für nächste