13.12.2021 komplexer Simplexalgorithmus#

  • bei nicht Standard-Maximum-Problemen muss eine zulässige Ecke gefunden werden

  • in der Praxis über künstliche Variablen

BSP 138:22-01-06_16-23

Einführung der küsntlichen Variablen:

  1. nicht-erlaubte 4. Ungleichung: \(IV:x_1+x_3 \ge 40\)

  2. Umformung \(IV*(-1):-x_1-x_3 \le -40\)

  3. Schlupfvariable: \(-x_1-x_3+y_4 = -40\)

  4. künstliche Variable (negativ!) \(-x_1-x_3+y_4 -y_5 = -40\)

  5. Umstellung nach küsntl. Variable: \(-y_5 = x_1+(0*x_2)+x_3-y_4 -40\)

    • wenn hier alle Variablen 0, dann \(-y_5 = -40 \to y_5 = 40\)

    • also Ziel = Minimierung y5

  6. Eintragung ins Tableau als Zeile: \(y_5 || \ 1\ |\ 0\ |\ 1\ |-1||\ 40\)

  7. Als Hilfszielformulierung \(z_h\)das negative der Spalte eintragen

  8. als erstes das Hilfsziel lösen!

    • also das negativste elemenet nehmen, q bilden, Pivotelement …

Darstellung des Tableaus: 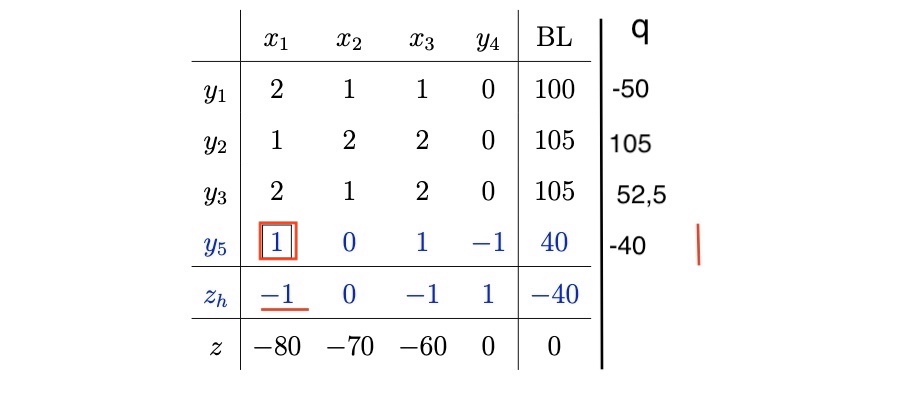21-12-14_12-24

Interpretaion des Endergebnises: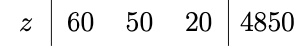21-12-14_12-27

  • Alle >= 0 = optimal

  • keine 0 = eindeutig

  • \(z = 4850-(60y_4+50y_3+20y_1)\)

    • die y-Koeffizienten sind die Opportunitätskosten der Produktion

    • steigende Opportunitätskosten = sinkender Gewinn